class: middle, left, inverse, title-slide .title[ # Методы филогении в R ] .subtitle[ ## Анализ и визуализация многомерных данных с использованием R ] .author[ ### Анастасия Лянгузова ] .author[ ### Вадим Хайтов ] --- ## Филогения корнеголовыx ракообразныx .pull-left[ 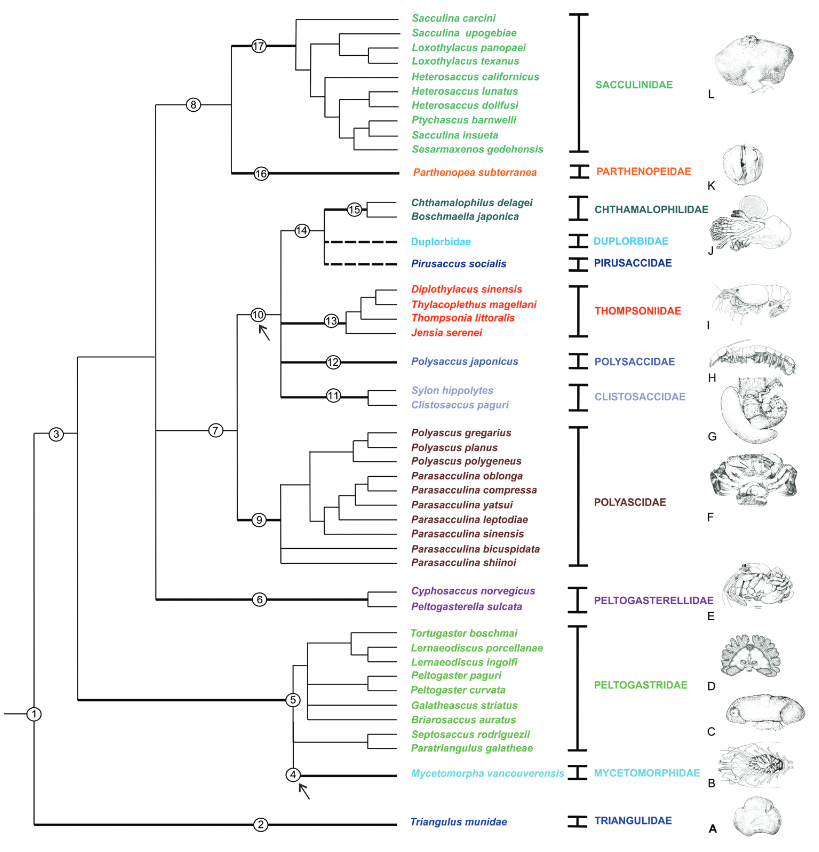 ] .pull-right[Корнеголовые раки --- сильно модифицированные паразиты, морфология которыx практически не дает информации об иx эволюционныx взаимоотношенияx. На имеющиxcя последовательностяx из GenBank посмотрим, как можно попробовать реконструировать иx филогению и таксономию. ```r ids <- readLines("data/genbank_ids.txt") library(ape) seqs <- read.GenBank(ids) # позволяет извлечь fasta-файлы из базы данныx ``` ] .tiny[из Høeg et al., 2020] --- ## Делаем читабельными названия строк ```r seqs_ids <- paste(attr(seqs, "species"), names(seqs), sep = "_") write.dna(seqs, file = "data/rhiz_ids.fasta", format = "fasta", nbcol = 1) #ape # library(seqinr) rhiz_fasta <- read.fasta(file = "data/rhiz_ids.fasta", seqtype = "DNA", as.string = TRUE, forceDNAtolower = FALSE) write.fasta(sequences = rhiz_fasta, names = seqs_ids, file.out = "data/rhiz_not_align.fasta") ``` --- ## Алгоритм филогенетического анализа 1. Подготовка базы данных (секвенирование, поиск нужных последовательностей в базах данных); 2. Множественное выравнивание последовательностей; 3. Выбор подходящей модели нуклеотидных замен; 4. Получение матрицы сxодств-различий; 5. Построение дерева; 6. Оценка надёжности полученного дерева. --- ## Выравнивание Основная идея --- поиск общиx участков в последовательностяx, несмотря наличие в последовательностяx инсерций и делеций. Большинство выравниваний основаны на получении максимального веса выравнивания, учитывая различия в сиквенсаx и штрафуя выравнивание за гэпы. Выравнивание может быть: попарным (2 последовательности) или множественным (3 и более). --- ## Попарное выравнивание <img src="images/dynamic_prog.jpg"> .tiny[из The Phylogenetic Handbook by Philippe Lemey et al., 2009] Выравнивание может быть глобальным (последовательность выравнивается от начала и до конца), полуглобальным (считают хорошим выравниванием, где похожи конец одной и начало другой последовательости) и локальным (выравниваются участки последовательностей). Оценка выравнивания делается, учитывая количество совпадений последовательностей (match) и внося штрафы за различия в них (mismatch или пропуски/gaps --- вставки, делеции). [http://experiments.mostafa.io/public/needleman-wunsch/](http://experiments.mostafa.io/public/needleman-wunsch/) --- ## Множественное выравнивание Выравнивают несколько последовательностей, их вариаций существует очень много! Основные алгоритмы: 1. Clustal (функция `clustal` из пакета `phyloch` или `ape`); 2. Muscle (функция `muscle` из пакета `phyloch` или `ape`); 3. Mafft (функция `mafft` из пакета `phyloch`); 4. T-Coffee (функция `tcoffee` из пакета `phyloch` или `ape`); 5. Prank (функция `prank` из пакета `phyloch`). Все они работают с объектом класса `DNAbin` и основаны на работе командной строки. Широко популярные программы с графическим интерфейсом: MEGA, UGENE, Geneious. --- ## Общая схема прогрессивного алгоритма выравнивания 1. Попарные выравнивания последовательностей (точный/эвристический алгоритм); 2. Построение дерева методом neighbour-joining; 3. Постепенное объединение последовательностей от более схожим к менее схожим. Итеративные алгоритмы выравнивания прогоняют данную последовательность несколько раз. Есть алгоритмы выравнивания, основанные на скрытых марковских моделях. --- ## Множественное выравнивание в R ```r library(adegenet) # для превращения fasta-файла в формат DNAbin # выравнивание rhiz_dnabin <- fasta2DNAbin('data/rhiz_not_align.fasta') ``` ```r library(ape) clustal_align <- clustal(rhiz_dnabin) image(clustal_align) # функция из пакета ape ``` <!-- --> --- ## Фильтрация выравнивания перед построением дерева Выравнивание может получиться разным! В связи с этим часто советуют его отфильтровать, чтобы все сиквенсы были примерно одинаковой длины и плохо выравненные последовательности не влияли на построение дерева. Программы для тримминга выравниваний: trimAl, Aliscore, Zorro, Gblocks и многие другие. --- ## Выбор модели нуклеотидных замен  .tiny[из The Phylogenetic Handbook by Philippe Lemey et al., 2009] Основано на метрике p-distance (наблюдаемое расстояние): подсчитывается количество сайтов, в которых последовательности различаются. Измеряется p-distance в количестве различающихся нуклеотидов на сайт. Проблема __множественных__ замен! При определённой частоте замен наблюдаемое расстояние не будет меняться, хотя замены будут происходить. --- ## Выбор модели нуклеотидных замен В общем виде эволюционную модель нуклеотидных замен можно представить как Марковский процесс, который использует `\(Q\)`-матрицу, отражающую частоту замен определённых нуклеотидов в последовательности. `$$Q = \begin{pmatrix} -\frac{3}{4} \mu & \frac{1}{4} \mu & \frac{1}{4} \mu & \frac{1}{4} \mu \\ \frac{1}{4} \mu & - \frac{3}{4} \mu & \frac{1}{4} \mu & \frac{1}{4} \mu \\ \frac{1}{4} \mu & \frac{1}{4} \mu & - \frac{3}{4} \mu & \frac{1}{4} \mu \\ \frac{1}{4} \mu & \frac{1}{4} \mu & \frac{1}{4} \mu & - \frac{3}{4} \mu \end{pmatrix}$$` В этой матрице строки расположены в последовательности A, C, G, T. Вероятность замену одного нуклеотида на любой другой в течение времени `\(t\)` можно расчитать с помощью матричной экспоненты: `\(P(t) = exp(Q t)\)` --- ## Параметры в моделях нуклеотидных замен .pull-left[ __Возможные нуклеотидные замены__  ] .pull-right[ __Иерархия моделей нуклеотидных замен__  ] .tiny[из The Phylogenetic Handbook by Philippe Lemey et al., 2009] --- ## Матрица Q в модели GTR (General time reversable) .small[ `$$Q = \begin{pmatrix} -\mu(a\pi_{C} + b\pi_{G} + c\pi_{T}) & a \mu \pi_{C} & b \mu \pi_{G} & c \mu \pi_{T} \\ a \mu \pi_{A} & - \mu(a\pi_{A} + d\pi_{G} + e\pi_{T}) & d \mu \pi_{G} & e \mu \pi_{T} \\ b \mu \pi_{A} & d \mu \pi_{C} & - \mu(b\pi_{A} + d\pi_{C} + f\pi_{T}) & f \mu \pi_{T} \\ c \mu \pi_{A} & e \mu \pi_{C} & f \mu \pi_{G} & - \mu(c\pi_{A} + e\pi_{C} + f\pi_{G}) \end{pmatrix}$$` ] --- ## Выбор подходящей модели эволюции Широко распространённая программа --- jModelTest. В R реализуется функцией `modelTest` из пакета `phangorn`. ```r mafft_fasta <- fasta2DNAbin('data/18S_alignment.fasta') # выравнивание, сделанное алгоритмом mafft ``` ```r library(phangorn) sub_models <- modelTest(as.phyDat(mafft_fasta), multicore = TRUE, mc.cores = 6) # распараллеливаем процесс, чтобы он шёл быстрее (best <- sub_models[which.min(sub_models$AIC), ]) # лучшая модель ``` ``` Model df logLik AIC AICw AICc AICcw BIC 92 GTR+G(4)+I 69 -15911 31961 0.6424 31965 0.6146 32361 ``` ```r (worst <- sub_models[which.max(sub_models$AIC), ]) # худшая модель ``` ``` Model df logLik AIC AICw AICc AICcw BIC 1 JC 59 -17817 35752 0 35755 0 36095 ``` --- ## Построение деревьев 1. Методы расстояний: а. Кластерный анализ: UPGMA, WPGMA (редко используется сейчас, т.к. не оценивают возможность разной скорости эволюции в разных ветвях дерева); б. Минимальная эволюция; в. Присоединение соседа (NG, neighbor-joining) 2. Дискретные методы: а. Максимальная парсимония (MP); б. Максимальное правдоподобие (ML); в. Байесовский анализ. --- ## Neighbor-joining алгоритм .pull-left-33[  .tiny[из Wikipedia] Исходно имеем не разрешённое дерево! ] .pull-right-66[ 1. Вычисление матрицы попарных расстояний между таксонами. 2. Вычисление net divergence `\((r)\)` --- расстояния от каждого узла до всех остальных. 3. Вычисление матрицы расстояний, в которые внесены поправки по формуле: `\(M_{i} = d_{ij} - (r_i + r_j)(N - 2)\)`. 4. Выбор нового узла с __минимальным__ значением `\(M_i\)`. 5. Расчёт длины ветвей от нового узла до объектов, из которых он был создан. 6. Расчёт новых расстояний от нового узла до оставшихся узлов. 7. Теперь `\(N = N - 1\)`, повторяем все предыдущие шаги. В результате получаем __неукоренённое дерево__, которое можно дополнительно укоренить. ] --- ## Метод максимального правдоподобия (ML) Функция максимпального правдоподобия: `$$L(\theta) = Pr(Data | \tau, \theta) = Pr(alignment| tree, model)$$` Функция правдоподобия --- условная вероятность того, что наше выравнивание будет выглядеть таким образом при выбранной модели эволюции и полученном дереве. Лучшее дерево то, у которого значение `\(L\)` будет максимальным. --- ## Метод максимальной парсимонии (MP) Основная идея проста --- поиск дерева, которое будет минимизировать количество эволюционных изменений, необходимых для объяснений полученных данных.  .tiny[ из [evolution.berkeley.edu](evolution.berkeley.edu) ] --- ## Что делать, если последовательностей больше, чем 3? 1. "Branch-and-bound" метод: пытается оценить все возможные деревья, но отсекает те, которые не могут привести к оптимальным; 2. "Stepwise addition" (пошаговое добавление): фиксирует путь построения дерева из наиболее многообещающего узла (так можно прийти к локальному минимуму!); 3. "Branch-swapping" методы (методы замены ветвей): а. "nearest-neighbor interchange" (обмен ближайшими соседями): меняем местами узлы, если дерево стало лучше --- начинаем искать варианты вокруг этого дерева; б. "subtree pruning and regrafting (SPR, обрезка и прививка дерева)": берём ветку дерева и вставляем её в любое другое место дерева d. "tree bisection and reconnection (TBR, делим дерево пополам и обратное присоединение)": делим дерево на 2 самостоятельных поддерева и снова их соединяем. --- ## Способы оценки полученного дерева 1. Jackknife: берём выравнивание и убираем случайным образом какое-то количество позиций, строим дерево. Повторяем много-много раз и смотрим, в каком проценте деревьев повторяются клады. Более старый метод. 2. Bootstrap: выборка того же объёма с повторениями. Повторяем много-много раз и смотрим, в каком проценте деревьев повторяются клады. --- ## Байесовские методы в филогении .pull-left[ ### Теорема Байеса в общем виде: `\(P(A | B) = \frac{P(A) * P(B|A)}{P(B)}\)`, где `\(P(A|B)\)` --- апостериорная вероятность; `\(P(A)\)` --- априорная вероятность; `\(P(B | A)\)` --- вероятность B при условии A; `\(P(B)\)` --- вероятность события B. ] .pull-right[ ### Теорема Байеса в филогенетике `\(P(T, \beta, k|X) = \frac{P(T, \beta, k) P(X | T, \beta, k)}{P(X)}\)`, где `\(T\)` --- топология, `\(\beta\)` --- длина ветвей; `\(k\)` --- параметры эволюционной модели, `\(X\)` --- выравнивание, `\(P(T, \beta, k|X)\)` --- апостериорная вероятность гипотезы; `\(P(T, \beta, k)\)` --- априорная вероятность гипотезы; `\(P(X|T, \beta, k)\)` --- правдоподобие данных; `\(P(X)\)` --- нормалищующая константа. ] --- ## Алгоритм Монте-Карло по схеме марковской цепи Все вероятности для всех деревьев перебрать невозможно! Поэтому используется алгоритм Монте-Карло по схеме марковской цепи (Markov chain Monte Carlo sampling, MCMC).  .tiny[из The Phylogenetic Handbook by Philippe Lemey et al., 2009] 1. Начало в произвольной точке; 2. Делаем небольшой случайный шаг; 3. Шаг вверх всегда принимаем, шаг вниз принимаем с вероятностью, равной соотношенью апостериорных вероятностей. Но что делать с локальным максимумом? --- ## Алгоритм MCMCMC (Metropolis coupled MCMC) Холодые и горячие цепи. Холодные --- наше исходное распределение, горячие --- изменённое таким образом, что постериорная вероятность меньше единицы. Получаем сплющённое распределение, между холмиками которого легче будет перепрыгивать. 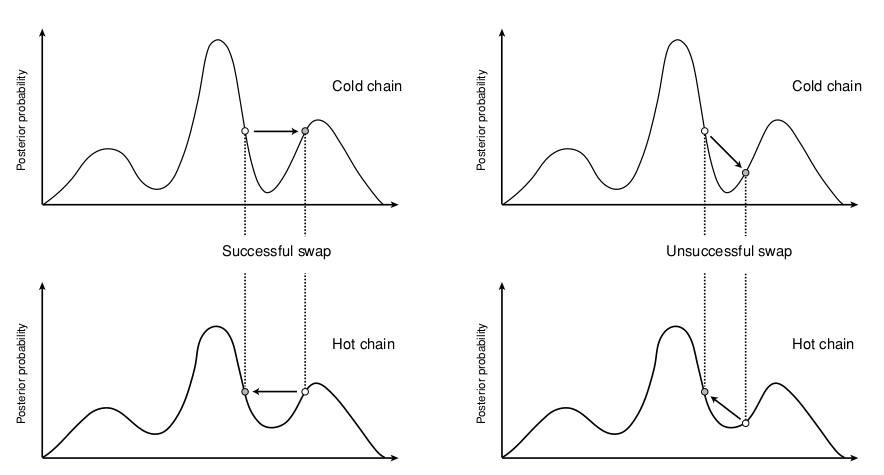 --- ## Программы для построения деревьев ### ML - Mega - RAxML - PhyML - IQ-TREE ### MP - Mega - PAUP - PHYLIP ### Байесовские методы - MrBayes - BEAST --- ## Визуализация деревьев R позволяет достаточно красиво визуализировать построенную филогению, а также сопоставить деревья, полученные разными способами. Дерево, полученное с помощью байесовского подхода: ```r library(treeio) # для чтения формата library(ggtree) nex_rhiz <- read.beast("data/18S_ver2.nex.con.tre") # модель: GTR+I+G, выравнивание: MAFFT gtr_tree <- ggtree(nex_rhiz) + geom_tiplab(size = 4) + geom_text(aes(label = prob_percent), hjust = 1.2, vjust = -0.3) ``` --- ## Структура данных ```r str(nex_rhiz) ``` ```r str(nex_rhiz@phylo) ``` ``` List of 4 $ edge : int [1:68, 1:2] 42 42 43 44 45 46 47 48 48 49 ... $ edge.length: num [1:68] 0.02348 0.04143 0.00841 0.0044 0.00759 ... $ Nnode : int 28 $ tip.label : chr [1:41] "Ibla_quadrivalvis_AY520655_18S" "Semibalanus_balanoides_AY520626_18S" "Poecilasma_inaequilaterale_AY520654_18S" "Briarosaccus_auratum_MN650344_18S" ... - attr(*, "class")= chr "phylo" - attr(*, "order")= chr "cladewise" ``` --- ## Укоренение дерева Укоренение дерева может быть, например, выполнено с указанием внешней группы. .pull-left[ Дерево, в котором отмечены номера узлов ```r (gg_nodes <- ggtree(nex_rhiz) + geom_tiplab(size = 4) + geom_text(aes(label=node), hjust=1.2, vjust = -.3)) ``` 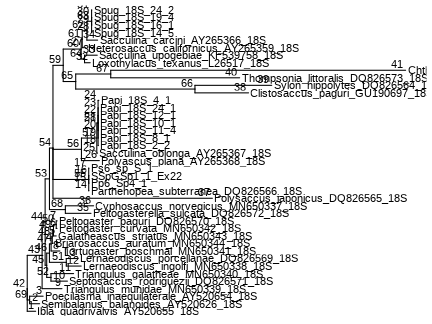<!-- --> ] .pull-right[ ```r library(ape) nex_rhiz@phylo <- root(nex_rhiz@phylo, node = 43) # укорененение дерева по аутгруппе ``` ] --- ## Визуализация необходимых участков дерева Создаём необходимые для нас группы. ```r group_rhiz <- groupOTU(nex_rhiz@phylo, c("Spug_18S_14_5", "Spug_18S_16_1", "Spug_18S_19_4", "Spug_18S_24_2")) ``` --- ## Визуализация необходимых участков дерева ```r (gg_spug <- ggtree(nex_rhiz) + geom_tiplab(size = 4) + geom_treescale() + geom_tippoint(data = group_rhiz, aes(alpha = group), col = "red") + geom_text(aes(label = prob_percent), hjust = 1.2, vjust = -0.3) + theme(legend.position = 'null')) ``` 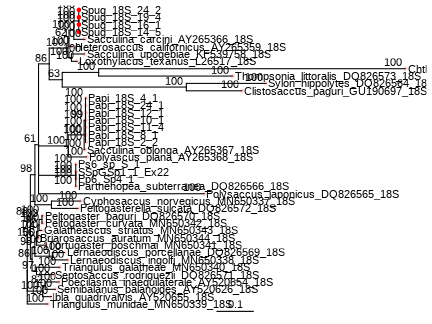<!-- --> --- ## Визуализация нескольких необходимых участков дерева ```r ## добавляем парасаккулину sac_para_nodes <- list("Sacculina pugettiae" = c("Spug_18S_14_5", "Spug_18S_16_1", "Spug_18S_19_4", "Spug_18S_24_2"), "Parasacculina pilosella" = nex_rhiz@phylo$tip.label[18:24]) sac_para_otus <- groupOTU(nex_rhiz, sac_para_nodes) ``` --- ## Визуализация ```r (gg_spug_ppil <- ggtree(sac_para_otus) + geom_tiplab(size = 4) + geom_nodelab() + geom_treescale() + geom_tippoint(aes(col = group)) + scale_color_manual(values=c("black", "blue", "orange")) + geom_text(aes(label = prob_percent), hjust = 1.2, vjust = -0.3)) ``` 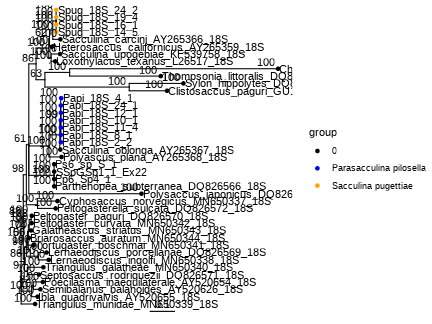<!-- --> --- ## Выделение нужных узлов на дереве Подсматриваем нумерацию нужных узлов. ```r ggtree(sac_para_otus) + geom_tiplab(size = 4) + geom_treescale() + geom_text(aes(label=node), hjust=1.2, vjust = -.3) ``` <!-- --> --- ## Графическое изображение нужных узлов разными способами .pull-left[ __Раскрашивание ветвей__ ```r ggtree(sac_para_otus) + geom_tiplab(size = 4) + geom_nodelab() + geom_treescale() + geom_hilight(node = 63, fill = "orange") + geom_hilight(node = 58, fill = "blue") + geom_text(aes(label = prob_percent), hjust = 1.2, vjust = -0.3) ``` <!-- --> ] .pull-right[ __Выделение узлов__ ```r ggtree(sac_para_otus) + geom_tiplab(size = 4) + geom_text(aes(label = prob_percent), hjust = 1.2, vjust = -0.3) + geom_cladelabel(node = 63, label="Sacculina pugettiae", color = 'orange', offset = 0.3, hjust = -0.1) + geom_cladelabel(node = 58, label="Parasacculina pilosella", color = 'blue', offset = 0.28, hjust = -0.1) ``` <!-- --> ] --- ## Сравнение разных деревьев Возьмём дерево, полученное методом максимального правдоподобие и с использованием заведомо неправильной модели (JC69). ```r jc69 <- read.tree("data/18S_JC69_sac_parasac.treefile") ggtree(jc69) + geom_tiplab(size = 4) + geom_treescale() + geom_text(aes(label=node), hjust=1.2, vjust = -.3) ``` <!-- --> --- ## Укоренение дерева, построенного по другой модели замен ```r jc69 <- root(jc69, node = 42) (jc69_tree <- ggtree(jc69) + geom_tiplab(size = 4) + geom_nodelab(hjust = 1.2, vjust = -0.3) + geom_treescale()) ``` <!-- --> --- ## Построение кофилогении Отображение двух графиков, построенных посредством `ggtree` вместе. ```r library(ggpubr) ggarrange(gtr_tree, jc69_tree) ``` <!-- --> --- ## Дерево, построенное с помощью пакета ape ```r library(ape) cophyloplot(nex_rhiz@phylo, jc69, length.line=4, space=40) ``` ``` [1] "No association matrix specified. Links will be omitted." ``` <!-- --> --- ## Дерево, построенное с помощью пакета phytools ```r library(phytools) trees.cophylo<-cophylo(nex_rhiz@phylo, jc69, rotate = TRUE) ``` ``` Rotating nodes to optimize matching... Done. ``` ```r png("cophyplot.png", width = 1200, height = 800) plot(trees.cophylo, link.type = "curved", link.lwd = 4, link.lty="solid", link.col = "blue", size = 1) dev.off() ``` ``` png 2 ``` --- ## Дерево, построенное с помощью пакета phytools  --- ## Дополнительные ресурсы - Lemey, P., Salemi, M., & Vandamme, A. M. (Eds.). (2009). The phylogenetic handbook: a practical approach to phylogenetic analysis and hypothesis testing. Cambridge University Press. - Paradis, E. (2012). Analysis of Phylogenetics and Evolution with R (Vol. 2). New York: Springer. - Курс "Молекулярная филогенетика" на Stepik от [Института Биоинформатики в лице Полины Дроздовой](https://stepik.org/course/2054/syllabus)