Кластерный анализ

.title[
# Кластерный анализ
]
.subtitle[
## Анализ и визуализация многомерных данных с использованием R
]
.author[
### Марина Варфоломеева
]
.author[
### Вадим Хайтов
]
.author[
### Анастасия Лянгузова
]

---

## Кластерный анализ

- Методы построения деревьев
- Методы кластеризации на основании расстояний
- Примеры для демонстрации и для заданий
- Кластерный анализ в R
- Качество кластеризации:
    - кофенетическая корреляция
    - ширина силуэта
    - поддержка ветвей
- Сопоставление деревьев: танглграммы
- Неиерархические методы кластеризации:
    - K-means
    - C-means
    - DBSCAN

---

### Вы сможете

- Выбирать подходящий метод агрегации (алгоритм кластеризации)
- Строить дендрограммы
- Оценивать качество кластеризации (кофенетическая корреляция, ширина силуэта, поддержка ветвей) 
- Сопоставлять дендрограммы, полученные разными способами, при помощи танглграмм

---

# Пример: Волки

---

## Пример: Волки

Морфометрия черепов у волков в Скалистых горах и в Арктике (Jolicoeur, 1959)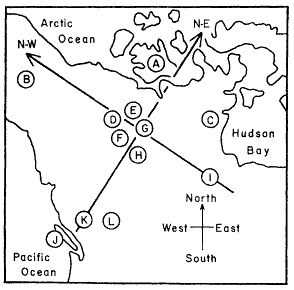

![Map from Jolicoeur 1959](images/Wolves_map_Jolicoeur_1959.png)

Данные взяты из работы Morrison (1990):

- A --- волки из Арктики (10 самцов, 6 самок)
- L --- волки из Скалистых гор (6 самцов, 3 самки)

```r
library(candisc)
data("Wolves")
```

---

## Знакомимся с данными

```r
dim(Wolves)
```

```
[1] 25 12
```

```r
colnames(Wolves)
```

```
 [1] "group"    "location" "sex"      "x1"       "x2"       "x3"       "x4"      
 [8] "x5"       "x6"       "x7"       "x8"       "x9"      
```

```r
head(rownames(Wolves))
```

```
[1] "rmm1" "rmm2" "rmm3" "rmm4" "rmm5" "rmm6"
```

```r
any(is.na(Wolves))
```

```
[1] FALSE
```

```r
table(Wolves$group)
```

```

ar:f ar:m rm:f rm:m 
   6   10    3    6 
```

---

## Задание

- Постройте ординацию nMDS данных
- Оцените качество ординации
- Обоснуйте выбор коэффициента
- Раскрасьте точки на ординации волков в зависимости от географического происхождения (`group`)

---

## Решение

```r
library(vegan)
library(ggplot2); theme_set(theme_bw(base_size = 16))
st_w <- scale(Wolves[, 4:ncol(Wolves)]) ## стандартизируем
ord_w <- metaMDS(comm = st_w, distance = "euclidean", autotransform = FALSE)
dfr_w <- data.frame(ord_w$points, Group = Wolves$group)
gg_w <- ggplot(dfr_w, aes(x = MDS1, y = MDS2)) + 
  geom_point(aes(colour = Group)) + 
  scale_color_manual(labels = c("Самки из Арктики", "Самцы из Арктики",
                                "Самки из Скалистых гор", 
                                "Самцы из скалистых гор"), 
                      values = c("red", "green", "blue", "purple")) +
  labs(colour = "Группы")
```

```
Run 0 stress 0.101 
Run 1 stress 0.1492 
Run 2 stress 0.1244 
Run 3 stress 0.101 
... New best solution
... Procrustes: rmse 0.000005603  max resid 0.00001869 
... Similar to previous best
Run 4 stress 0.1357 
Run 5 stress 0.1244 
Run 6 stress 0.101 
... Procrustes: rmse 0.000004521  max resid 0.00001452 
... Similar to previous best
Run 7 stress 0.101 
... Procrustes: rmse 0.0000125  max resid 0.00004729 
... Similar to previous best
Run 8 stress 0.101 
... Procrustes: rmse 0.000006085  max resid 0.00002023 
... Similar to previous best
Run 9 stress 0.1492 
Run 10 stress 0.101 
... Procrustes: rmse 0.000002464  max resid 0.000007485 
... Similar to previous best
Run 11 stress 0.1382 
Run 12 stress 0.1403 
Run 13 stress 0.1275 
Run 14 stress 0.1415 
Run 15 stress 0.1389 
Run 16 stress 0.1281 
Run 17 stress 0.128 
Run 18 stress 0.1511 
Run 19 stress 0.101 
... Procrustes: rmse 0.000001249  max resid 0.000003076 
... Similar to previous best
Run 20 stress 0.1412 
*** Best solution repeated 6 times
```
]

---

## Решение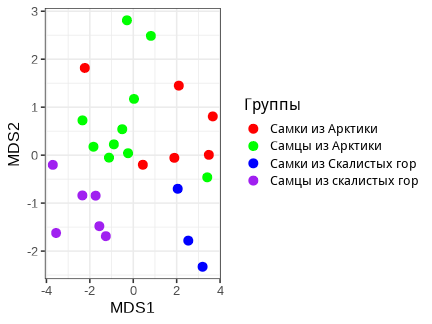

![](05_cluster_analysis_files/figure-html/fig-wolves-1.png)

---

## Методы кластеризации

- методы построения деревьев (о них следующие слайды)
]

- метод K-среднмх (K-means clustering) 
- метод нечёткой кластеризации C-средних (C-means clustering, fuzzy clustering)
- Основанная на плотности пространственная кластеризация для приложений с шумами (Density-based spatial clustering of applications with noise, DBSCAN)

]

---

## Какие бывают методы построения деревьев?

### Методы кластеризации на основании расстояний (о них сегодня)
  - Метод ближайшего соседа
  - Метод отдаленного соседа
  - Метод среднегруппового расстояния
  - Метод Варда
  - и т.д. и т.п.

### Методы кластеризации на основании признаков
  - Метод максимальной бережливости
  - Метод максимального правдоподобия

### И это еще далеко не всё!

---

# Методы кластеризации на основании расстояний

---

## Этапы кластеризации

.pull-left[
<div class="DiagrammeR html-widget html-fill-item" id="htmlwidget-211ed111e2e72d084e90" style="width:432px;height:540px;"></div>
<script type="application/json" data-for="htmlwidget-211ed111e2e72d084e90">{"x":{"diagram":"graph TD; \n           A(Набор признаков)-->B(Матрица расстояний или сходств); \n           B-->C(Группировка объектов);\n           C-->D(Отношения между кластерами); D-->E(Поправки); E-->A;\n           style A fill:#C6FFE7,stroke:#C6FFE7;\n           style B fill:#C6FFE7,stroke:#C6FFE7;\n           style C fill:#C6FFE7,stroke:#C6FFE7;\n           style D fill:#C6FFE7,stroke:#C6FFE7;\n           style E fill:#C6FFE7,stroke:#C6FFE7;\n           style A color:#C6FFE7,stroke:#C6FFE7;\n  "},"evals":[],"jsHooks":[]}</script>
]

Результат кластеризации зависит от

- выбора признаков
- коэффициента сходства-различия
- от алгоритма кластеризации

]

---

## Методы кластеризации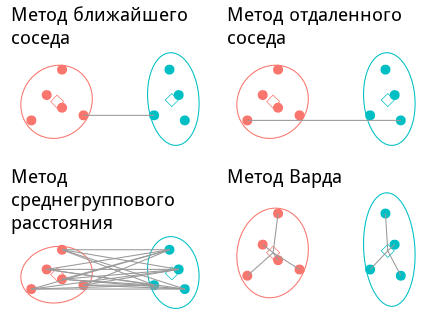

![](05_cluster_analysis_files/figure-html/fig-cluster-methods-1.png)

---

## Метод ближайшего соседа

__= nearest neighbour = single linkage__

- к кластеру присоединяется ближайший к нему кластер/объект
- кластеры объединяются в один на расстоянии, которое равно расстоянию между ближайшими объектами этих кластеров
]
]

![](05_cluster_analysis_files/figure-html/fig-single-1.png)
]

### Особенности

- Может быть сложно интерпретировать, если нужны группы
  - объекты на дендрограмме часто не образуют четко разделенных групп
  - часто получаются цепочки кластеров (объекты присоединяются как бы по одному)
- Хорош для выявления градиентов

---

## Как работает метод ближайшего соседа

![](05_cluster_analysis_files/figure-html/fig-single-guess-1.png)

---

## Как работает метод ближайшего соседа

![](05_cluster_analysis_files/figure-html/single-ani-.gif)

---

## Метод отдаленного соседа

__= furthest neighbour = complete linkage__

- к кластеру присоединяется отдаленный кластер/объект
- кластеры объединяются в один на расстоянии, которое равно расстоянию между самыми отдаленными объектами этих кластеров (следствие — чем более крупная группа, тем сложнее к ней присоединиться)
]]

![](05_cluster_analysis_files/figure-html/fig-complete-1.png)

]

### Особенности

- На дендрограмме образуется много отдельных некрупных групп
- Хорош для поиска дискретных групп в данных

---

## Как работает метод отдаленного соседа

![](05_cluster_analysis_files/figure-html/fig-complete-guess-1.png)

---

## Как работает метод отдаленного соседа

![](05_cluster_analysis_files/figure-html/complete-ani-.gif)

---

## Метод невзвешенного попарного среднего

__= UPGMA = Unweighted Pair Group Method with Arithmetic mean__

- кластеры объединяются в один на расстоянии, которое равно среднему значению всех возможных расстояний между объектами из разных кластеров.
]]
.pull-right-33[

![](05_cluster_analysis_files/figure-html/fig-average-1.png)

]

### Особенности

- UPGMA и WUPGMС иногда могут приводить к инверсиям на дендрограммах
.pull-left-66[
![Инверсии на дендрограммах](images/clust-revert.png)
]
.pull-right-33[
.pull-down[
из Borcard et al., 2011
]]

---

## Как работает метод среднегруппового расстояния

![](05_cluster_analysis_files/figure-html/average-ani-.gif)

---

## Метод Варда

__= Ward's Minimum Variance Clustering__

- объекты объединяются в кластеры так, чтобы внутригрупповая дисперсия расстояний была минимальной.
]

![](05_cluster_analysis_files/figure-html/fig-ward-1.png)
]
.pull-left-33[
### Особенности

- метод годится и для неевклидовых расстояний несмотря на то, что внутригрупповая дисперсия расстояний рассчитывается так, как будто это евклидовы расстояния.]

---

## Как работает метод Варда

![](05_cluster_analysis_files/figure-html/ward-ani-.gif)

---

# Кластерный анализ в R

---

## Кластеризация

Давайте построим деревья при помощи нескольких алгоритмов кластеризации (по стандартизованным данным, с использованием Евклидова расстояния) и сравним их.

```r
# Пакеты для визуализации кластеризации
library(ape)
library(dendextend)
```

```r
# Матрица расстояний
d <- dist(x = st_w, method = "euclidean")
```

---

## (1.0) Метод ближайшего соседа + `base`

```r
hc_single <- hclust(d, method = "single")
plot(hc_single)
```

![](05_cluster_analysis_files/figure-html/fig-single-base-1.png)

---

## (1.1) Метод ближайшего соседа + `ape`

```r
ph_single <- as.phylo(hc_single)
plot(ph_single, type = "phylogram")
axisPhylo()
```

![](05_cluster_analysis_files/figure-html/fig-single-ape-1.png)

---

## (1.2) Метод ближайшего соседа + `dendextend`

```r
den_single <- as.dendrogram(hc_single)
plot(den_single, horiz = TRUE)
```

![](05_cluster_analysis_files/figure-html/fig-single-dend-1.png)

---

## (2.1) Метод отдаленного соседа + `ape`

```r
hc_compl <- hclust(d, method = "complete")
ph_compl <- as.phylo(hc_compl)
plot(ph_compl, type = "phylogram")
axisPhylo()
```

![](05_cluster_analysis_files/figure-html/fig-complete-ape-1.png)

---

## (2.2)Метод отдаленного соседа + `dendextend`

```r
den_compl <- as.dendrogram(hc_compl)
plot(den_compl, horiz = TRUE)
```

![](05_cluster_analysis_files/figure-html/fig-complete-dend-1.png)

---

## (3.1) Метод невзвешенного попарного среднего (UPGMA) + `ape`

```r
hc_avg <- hclust(d, method = "average")
ph_avg <- as.phylo(hc_avg)
plot(ph_avg, type = "phylogram")
axisPhylo()
```

![](05_cluster_analysis_files/figure-html/fig-average-ape-1.png)

---

## (3.2) Метод невзвешенного попарного среднего (UPGMA) + `dendextend`

```r
den_avg <- as.dendrogram(hc_avg)
plot(den_avg, horiz = TRUE)
```

![](05_cluster_analysis_files/figure-html/fig-average-dend-1.png)

---

## (4.1) Метод Варда + `ape`

```r
hc_w2 <-hclust(d, method = "ward.D2")
ph_w2 <- as.phylo(hc_w2)
plot(ph_w2, type = "phylogram")
axisPhylo()
```

![](05_cluster_analysis_files/figure-html/fig-ward-ape-1.png)

---

## (4.2) Метод Варда + `dendextend`

```r
den_w2 <- as.dendrogram(hc_w2)
plot(den_w2, horiz = TRUE)
```

![](05_cluster_analysis_files/figure-html/fig-ward-dend-1.png)

---

# Качество кластеризации

---

## Кофенетическая корреляция

__Кофенетическое расстояние__  — расстояние между объектами на дендрограмме, т.е. то расстояние, на котором объекты становятся частью одной группы в ходе процесса кластеризации.

.content-box-green[
__Кофенетическая корреляция__  — мера качества отображения многомерных данных на дендрограмме. Кофенетическую корреляцию можно рассчитать как Пирсоновскую корреляцию (обычную) между матрицами исходных и кофенетических расстояний между всеми парами объектов. В идеальном случае равна 1. 
]

<br/>

Метод агрегации, который дает наибольшую кофенетическую корреляцию, дает кластеры, лучше всего отражающие исходные данные.

Матрицу кофенетических расстояний и кофенетическую корреляцию можно рассчитать при помощи функций из пакета `stats` (`dendextend`) и `ape`, соответственно.

---

## Кофенетическая корреляция в R

```r
# Матрица кофенетических расстояний 
c_single <- cophenetic(ph_single)

# Кофенетическая корреляция = 
# = корреляция матриц кофенетич. и реальн. расстояний
cor(d, as.dist(c_single))
```

```
[1] 0.5654
```

---

## Задание:

Оцените при помощи кофенетической корреляции качество кластеризаций, полученных разными методами.

Какой метод дает лучший результат?

---

## Решение:

```r
c_single <- cophenetic(ph_single)
cor(d, as.dist(c_single))
```

```
[1] 0.5654
```

```r
c_compl <- cophenetic(ph_compl)
cor(d, as.dist(c_compl))
```

```
[1] 0.7058
```

```r
c_avg <- cophenetic(ph_avg)
cor(d, as.dist(c_avg))
```

```
[1] 0.7447
```

```r
c_w2 <- cophenetic(ph_w2)
cor(d, as.dist(c_w2))
```

```
[1] 0.726
```

---

## Что можно делать дальше с дендрограммой

- Можно выбрать число кластеров: 
    + либо субъективно, на любом выбранном уровне (главное, чтобы кластеры были осмысленными и интерпретируемыми);
    + либо исходя из распределения расстояний ветвления.
- Можно оценить стабильность кластеризации при помощи бутстрепа.

---

## Ширина силуэта

.content-box-green[
Ширина силуэта `$s_i$` --- мера степени принадлежности объекта `$i$` к кластеру 
]

`$$s_i = \frac {\color{purple}{\bar{d}_{i~to~nearest~cluster}} - \color{green}{\bar{d}_{i~within}}} {max\{\color{purple}{\bar{d}_{i~to~nearest~cluster}}, \color{green}{\bar{d}_{i~within}}\}}$$`

`$s_i$` --- сравнивает между собой средние расстояния от данного объекта:
- `$\color{green} {\bar{d}_{i~within}}$` --- до других объектов из того же кластера
- `$\color{purple} {\bar{d}_{i~to~nearest~cluster}}$` --- до ближайшего кластера

`$-1 \le s_i \le 1$` --- чем больше `$s_i$`, тем "лучше" объект принадлежит кластеру.

- Средняя ширина силуэта для всех объектов из кластера --- оценивает, насколько "тесно" сгруппированы объекты.
- Средняя ширина силуэта по всем данным --- оценивает общее качество классификации.
- Чем больше к 1, тем лучше. Если меньше 0.25, то можно сказать, что нет структуры.

---

## Как рассчитывается ширина силуэта

Оценим ширину силуэта для 3 кластеров

```r
library(cluster)
avg3 <- cutree(tree = hc_avg, k = 3) # делим дерево на нужное количество кластеров
plot(silhouette(x = avg3, dist = d), cex.names = 0.6)
```

![](05_cluster_analysis_files/figure-html/fig-silhouette-1.png)

---

## Бутстреп

.content-box-green[
__Бутстреп__ --- один из методов оценки значимости полученных результатов; повторная выборка из имеющихся данных. В такой выборке элементы могут повторяться.]

### Алгоритм
- Имеющиеся данные делим на группы одинакового размера: какие-то элементы могут отсутствовать, а какие-то --- повторяться несколько раз. 
- На основе полученных данных строим дендрограмму. 
- Повторяем всё много раз.

---

## Бутстреп поддержка ветвей

> "An approximately unbiased test of phylogenetic tree selection."
>
> --- Shimodaria, 2002

Этот тест использует специальный вариант бутстрепа --- multiscale bootstrap. Мы не просто многократно берем бутстреп-выборки и оцениваем для них вероятность получения топологий (BP p-value), эти выборки еще и будут с разным числом объектов. По изменению BP при разных объемах выборки можно вычислить AU (approximately unbiased p-value).

```r
library(pvclust)
set.seed(389)
# итераций должно быть 1000 и больше, здесь мало для скорости
cl_boot <- pvclust(t(st_w), method.hclust = "average", nboot = 100, 
                   method.dist = "euclidean", parallel = TRUE, iseed = 42)
```

```
Creating a temporary cluster...done:
socket cluster with 11 nodes on host 'localhost'
Multiscale bootstrap... Done.
```

Обратите внимание на число итераций: `nboot = 100` --- это очень мало. На самом деле нужно 10000 или больше.

---

## Дерево с величинами поддержки

AU --- approximately unbiased p-values (красный),
BP --- bootstrap p-values (зеленый)

```r
plot(cl_boot)
pvrect(cl_boot) # достоверные ветвления
```

![](05_cluster_analysis_files/figure-html/fig-cl-boot-1.png)

---

## Для диагностики качества оценок AU

График стандартных ошибок для AU p-value нужен, чтобы оценить точность оценки самих AU. Чем больше было бутстреп-итераций, тем точнее будет оценка AU.

```r
seplot(cl_boot)
# print(cl_boot) # все значения
```

![](05_cluster_analysis_files/figure-html/fig-seplot-1.png)

---

# Сопоставление деревьев: Танглграммы

---

## Танглграмма

Два дерева (с непохожим ветвлением) выравнивают, вращая случайным образом ветви вокруг оснований. Итеративный алгоритм. Картина каждый раз разная.

```r
set.seed(395)
untang_w <- untangle_step_rotate_2side(den_compl, den_w2, print_times = F)

# танглграмма
tanglegram(untang_w[[1]], untang_w[[2]],
           highlight_distinct_edges = FALSE,
           common_subtrees_color_lines = F,
           main = "Tanglegram",
           main_left = "Left tree",
           main_right = "Right tree",
           columns_width = c(8, 1, 8),
           margin_top = 3.2, margin_bottom = 2.5,
           margin_inner = 4, margin_outer = 0.5,
           lwd = 1.2, edge.lwd = 1.2, 
           lab.cex = 1.5, cex_main = 2)
```

---

## Танглграмма

![](05_cluster_analysis_files/figure-html/fig-tang-1.png)

---

## Задание

Постройте танглграмму из дендрограмм, полученных методом ближайшего соседа и методом Варда.

---

## Раскраска дендрограмм

### Вручную

```r
# Произвольные цвета радуги
cols <- rainbow(30) 
den_avg_manual <- color_labels(dend = den_avg, col = cols)
plot(den_avg_manual, horiz = TRUE)
```

![](05_cluster_analysis_files/figure-html/unnamed-chunk-9-1.png)

---

## Раскраска дендрограмм

### С помощью функции

```r
# Функция для превращения лейблов в цвета
# (группы определяются по `n_chars` первых букв в лейбле)
get_colours <- function(dend, n_chars, palette = "Dark2"){
  labs <- get_leaves_attr(dend, "label")
  group <- substr(labs, start = 0, stop = n_chars)
  group <- factor(group)
  cols <- brewer.pal(length(levels(group)), name = palette)[group]
  return(cols)
}
```
]

```r
library(RColorBrewer)
cols <- get_colours(dend = den_avg, n_chars = 3)
den_avg_c <- color_labels(dend = den_avg, col = cols)
plot(den_avg_c, horiz = TRUE)
```

![](05_cluster_analysis_files/figure-html/unnamed-chunk-11-1.png)
]
---

## Неиерархические методы кластеризации

---

## Метод K-средних (K-means)

.pull-right[
В отличие от иерархических методов кластеризации K-means будет искать то количество кластеров (k), которое вы ему зададите. Каждое наблюдение принадлежит кластеру с ближайшим значением среднего числа (центроида); помимо этого K-means кластеризация минимизирует разброс значений внутри каждого из кластера.

Используется в машинном обучении, в том числе, например, для цветовой редуцкии изображений. 
]

---

## Алгоритм K-means

.pull-left[
### График наблюдений 
![](05_cluster_analysis_files/figure-html/unnamed-chunk-13-1.png)

Здесь как будто бы выделяются 3 кластера, поэтому возьмём k = 3. Что же будет делать алгоритм?
]

Например, так:

![](05_cluster_analysis_files/figure-html/unnamed-chunk-14-1.png)
]

---

## Алгоритм K-means

При этом каждая точка приписывается к ближайшему кластеру.

![](05_cluster_analysis_files/figure-html/unnamed-chunk-15-1.png)
]

![](05_cluster_analysis_files/figure-html/unnamed-chunk-16-1.png)
]

---

## 4. Расчёт расстояний от каждой точки до нового центроида

![](05_cluster_analysis_files/figure-html/unnamed-chunk-17-1.png)
]

.pull-right[
Разброс считается как сумма квадратов расстояний между отдельными наблюдениями и центроидом.

$$ \sum_{i=1}^{n}(x_i - \overline{x})$$
]

---

## 5. Повторяем всё многократно до тех пор, пока разброс не станет минимальным

Кластеры с минимальным разбросом --- финальные.

![](05_cluster_analysis_files/figure-html/unnamed-chunk-18-1.png)

---

## Поиск локального минимума

![:scale 50%](images/kmeans_algorithm_local.png)
.tiny[
Из Legendre, Legendre, 2012
]

Кратко алгоритм можно свести к поиску общего минимума среди локальных (вне зависимости от начальной конфигурации).

---

## K-means в R

Если в данных много нулей, их обязательно нужно стандартизовать (что мы уже делали).

K-means кластеризацию в R делает функция `kmeans` (пакет `stats`), ей нужно передать аргументы `centers` (количество кластеров) и `nstart`(количество случайных итераций).

```r
set.seed(333)
w_kmeans <- kmeans(st_w, centers = 3, nstart = 100)
```
Полученные результаты можно сравнить с тем, что нам дала иерархическая кластеризация (UPGMA) --- оценка ширины силуэта.

```r
table(avg3, w_kmeans$cluster)
```

```
    
avg3 1 2 3
   1 6 0 9
   2 0 7 0
   3 0 1 2
```

---

## Как выбрать нужное количество кластеров?

Два популярных критерия:

- Индекс Калински-Харабаза (Calinski–Harabasz index): F-статистика, сравнивающая меж- и внутригрупповую сумму квадратов. Если группы одинаковой величины

- Индекс простой структуры (Simple Structure Index): оценивает влияние на интепретабельность полученной кластеризации. Если группы разной величины

---

## Как выбрать нужное количество кластеров?

Функция `cascadeKM` из пакета `vegan`. По сути функция-обёртка, которая проводит кластеризацию с разным заданным количеством кластеров.

```r
w_cascade <- cascadeKM(st_w, inf.gr = 2, sup.gr = 10, 
                       iter = 100, criterion = 'calinski')
```

- `inf.gr` --- начальное количество кластеров,
- `sup.gr` --- максимальное количество кластеров,
- `iter` --- количество итераций для каждой кластеризации,
- `criterion` --- индекс: `calinski` или `ssi`.

---

## Визуализация результатов множественной кластеризации

```r
plot(w_cascade, sortg = TRUE) # чтобы объекты, относящиеся к одному кластеру, рисовались вместе
```

![](05_cluster_analysis_files/figure-html/unnamed-chunk-22-1.png)

Советует 2 кластера!

---

## Визуализация k-means

Делается с помощью функции `fviz_cluster` из пакета `factoextra`.

```r
library(factoextra)
fviz_cluster(w_kmeans, data = st_w,
             ggtheme = theme_bw())
```

![](05_cluster_analysis_files/figure-html/unnamed-chunk-23-1.png)
]

```r
w_2k <- kmeans(st_w, centers = 2, 
               nstart = 100)

fviz_cluster(w_2k, data = st_w,
             ggtheme = theme_bw())
```

![](05_cluster_analysis_files/figure-html/unnamed-chunk-24-1.png)
]

---

## Оценка качества кластеризации: ширина силуэта

```r
plot(silhouette(w_kmeans$cluster, d))
```

![](05_cluster_analysis_files/figure-html/unnamed-chunk-25-1.png)
]

```r
plot(silhouette(w_2k$cluster, d))
```

![](05_cluster_analysis_files/figure-html/unnamed-chunk-26-1.png)
]

---

## Density-based spatial clustering of applications with noise (DBSCAN)

.pull-left[
Основанная на плотности пространственная кластеризация для приложений с шумами --- метод, более подходящий для "вложенных" кластеров. Основан на распределении плотности точек.

![](05_cluster_analysis_files/figure-html/unnamed-chunk-27-1.png)
]

.pull-right[
Работает с данными, с которыми другие методы кластеризации не могут справиться (K-means в примере).

```r
set.seed(123)
circle_kmeans <- kmeans(multi, centers = 2, nstart = 20)
my_col_circle <- c("#2E9FDF", "#E7B800")
fviz_cluster(circle_kmeans, data = multi,
             palette = my_col_circle)
```

![](05_cluster_analysis_files/figure-html/unnamed-chunk-28-1.png)
]

---

## Принцип работы DBSCAN

Кластеры выбираются на основе плотности расположения точек. В результате в единый кластер объединяются близко расположенные друг к другу точки.

Задаваемые параметры:
- радиус расстояния, на котором должны рассматриваться близлежащие точки (`eps`)
- минимальное количество точек, которые расположены в круге этого радиуса (`minPts`)

Сore points --- точки, от которых можем присоединять в кластер новые точки и рядом с которыми расположено `minPts` количество точек.

Пограничные точки --- те, на которых кластер заканчивается.

Остальные точки считаются шумом и выбросами.

---

## DBSCAN в R

Провести такую кластеризацию можно с помощью функции `dbscan` из пакета `dbscan`.

![](05_cluster_analysis_files/figure-html/unnamed-chunk-29-1.png)

---

## Epsilon --- выбираем расстояние для радиуса

**График k-расстояний (k-distance plot)**

1. Вычисляется среднее значение расстояний каждой точки до ее k ближайших соседей.

2. k-расстояния отображаются в порядке возрастания.

Если на графике есть "колено" --- значительный перегиб, будет легко найти нужное значение радиуса. 
.pull-left[

```r
kNNdistplot(multi, k = 5)
abline(h = 0.23, lty = 2)
```

![](05_cluster_analysis_files/figure-html/unnamed-chunk-30-1.png)
]
.pull-right[

```r
circle_dbscan <- dbscan(multi, 0.23, 5)
fviz_cluster(circle_dbscan, data = multi,
             palette = my_col_circle)
```

![](05_cluster_analysis_files/figure-html/unnamed-chunk-31-1.png)
]

---

## Задание 4

Кластеризуйте данные по волкам, используя DBSCAN-алгоритм.

---

## Примерное решение

```r
kNNdistplot(st_w, k = 4)
abline(h = 2.4, lty = 2) 
```

![](05_cluster_analysis_files/figure-html/unnamed-chunk-32-1.png)
]

```r
w_dbscan <- dbscan(st_w, 2.4, 4)
fviz_cluster(w_dbscan, data = st_w)
```

![](05_cluster_analysis_files/figure-html/unnamed-chunk-33-1.png)
]

---

## Метод нечёткой кластеризации C-средних (C-means, fuzzy clustering)

При данном подходе объект необязательно принадлежит одному кластеру. Каждому объекту присваивается вероятность принадлежности к кластеру (membership value). В сумме все значения принадлежности к кластеру дают 1 для каждого из объектов.

---

## Алгоритм C-means

1. Каждому объекту приписывается случайное значение принадлежности к кластеру.

2. Рассчитываются центроиды для каждого кластера:

`$$\hat{v}_{i} = \frac{\sum^{N}_{k=1}(\hat{u}_{ik})^{m}y_k}{\sum^{N}_{k=1}(\hat{u}_{ik})^m}$$`

где `$\hat{u}$` --- значение принадлежности к кластеру, `$m$` --- параметр размытости (fuzziness), равный обычно 2, `$y_k$` --- конкретный объект, N --- количество объектов.

---

## Алгоритм C-means

<li> Расчёт расстояния от каждой точки до центроида.

<li> Обновление значений принадлежности к кластерам.

</ol>

`$$\hat{u}_{ik} = (\sum^{c}_{j=1}(\frac{\hat{d}_{ik}}{\hat{d}_{jk}})^{\frac{2}{m-1}})^{-1}$$`
где `$d_{ki}$` --- расстояние от точки до центроида.

<li> Повторить шаги с 2 по 4, пока не будут получены постоянные значения принадлежности к кластеру.

</ol>

---

## Кластеризация C-means в R

Есть несколько функций из разных пакетов, реализующих кластеризацию С-средних (например `fanny` из `cluster`, `cmeans` из `e1071`, `fcm` из `ppclust` и т.д.). Мы воспользуемся функцией `fanny` из пакета `cluster`.

Функция funny принимает как исходные данные, так и матрицу расстояний.

```r
w_cmeans <- fanny(d, k = 4, memb.exp = 2)
summary(w_cmeans)
```

```
Fuzzy Clustering object of class 'fanny' :                   
m.ship.expon.     2
objective     12.07
tolerance     1e-15
iterations       85
converged         1
maxit           500
n                25
Membership coefficients (in %, rounded):
      [,1] [,2] [,3] [,4]
rmm1    28   17   28   28
rmm2    28   16   28   28
rmm3    28   16   28   28
rmm4    29   14   29   29
rmm5    29   14   29   29
rmm6    28   17   28   28
rmf1    20   39   20   20
rmf2    21   37   21   21
rmf3    22   35   22   22
arm1    25   24   25   25
arm2    28   17   28   28
arm3    27   18   27   27
arm4    28   16   28   28
arm5    28   15   28   28
arm6    29   14   29   29
arm7    29   14   29   29
arm8    26   21   26   26
arm9    26   21   26   26
arm10   21   38   21   21
arf1    21   36   21   21
arf2    20   40   20   20
arf3    25   24   25   25
arf4    22   33   22   22
arf5    27   18   27   27
arf6    21   38   21   21
Fuzzyness coefficients:
dunn_coeff normalized 
   0.26251    0.01667 
Closest hard clustering:
 rmm1  rmm2  rmm3  rmm4  rmm5  rmm6  rmf1  rmf2  rmf3  arm1  arm2  arm3  arm4  arm5 
    1     1     1     1     1     1     2     2     2     3     3     3     1     1 
 arm6  arm7  arm8  arm9 arm10  arf1  arf2  arf3  arf4  arf5  arf6 
    1     1     3     3     2     2     2     3     2     1     2 
k_crisp (= 3) < k !!

Silhouette plot information:
      cluster neighbor sil_width
rmm4        1        3  0.364448
rmm2        1        3  0.354519
rmm3        1        3  0.348120
rmm5        1        3  0.312708
rmm1        1        3  0.290835
arm5        1        3  0.209294
arm6        1        3  0.190407
rmm6        1        3  0.137320
arf5        1        3  0.042882
arm7        1        3 -0.001203
arm4        1        3 -0.005208
arf2        2        3  0.391057
rmf2        2        3  0.347725
arm10       2        3  0.343759
rmf3        2        3  0.341740
arf6        2        3  0.312072
rmf1        2        3  0.268000
arf1        2        3  0.200487
arf4        2        3 -0.049651
arm1        3        2  0.259831
arm8        3        1  0.233975
arm9        3        1  0.192208
arm3        3        1  0.132853
arf3        3        2  0.083143
arm2        3        1  0.054878
Average silhouette width per cluster:
[1] 0.2040 0.2694 0.1595 0.2060
Average silhouette width of total data set:
[1] 0.2142

Available components:
 [1] "membership"  "coeff"       "memb.exp"    "clustering"  "k.crisp"    
 [6] "objective"   "convergence" "diss"        "call"        "silinfo"    
```

---

## Оценка качества кластеризации: ширина силуэта

```r
plot(silhouette(w_cmeans), cex.names = 0.6)
```

![](05_cluster_analysis_files/figure-html/unnamed-chunk-35-1.png)

Получилась не очень качественная кластеризация.

---

## Задание 5

Попробуйте оценить ширину силуэта для C-means кластеризации с более подходящим числом кластеров.

---

## Решение

```r
w_2means <- fanny(d, k = 2, memb.exp = 2)
plot(silhouette(w_2means), cex.names = 0.6)
```

![](05_cluster_analysis_files/figure-html/unnamed-chunk-36-1.png)

---

## Визуализация кластеризации

Для визуализации возьмём нашу исходную ординацию nMDS.

```r
library(scatterpie)
w_clust <- cbind(dfr_w, w_2means$membership)
ggplot() + geom_scatterpie(data = w_clust, aes(x = MDS1, y = MDS2),
                           cols = c("1", "2"))
```

![](05_cluster_analysis_files/figure-html/unnamed-chunk-37-1.png)

---

## Take-home messages

- Результат кластеризации зависит не только от выбора коэффициента, но и от выбора алгоритма.
- Качество кластеризации можно оценить разными способами.
- Кластеризации, полученные разными методами, можно сравнить на танглграммах.

---

## Дополнительные ресурсы

- Borcard, D., Gillet, F., Legendre, P., 2011. Numerical ecology with R. Springer.
- Legendre, P., Legendre, L., 2012. Numerical ecology. Elsevier.
- Quinn, G.G.P., Keough, M.J., 2002. Experimental design and data analysis for biologists. Cambridge University Press.

---

## И еще ресурсы

Как работает UPGMA можно посмотреть здесь:

- http://www.southampton.ac.uk/~re1u06/teaching/upgma/

Как считать поддержку ветвей (пакет + статья):

- pvclust: An R package for hierarchical clustering with p-values [WWW Document], n.d. URL http://www.sigmath.es.osaka-u.ac.jp/shimo-lab/prog/pvclust/ (accessed 11.7.14).

Для анализа молекулярных данных:

- Paradis, E., 2011. Analysis of Phylogenetics and Evolution with R. Springer.

Статья про C-means кластеризацию:

- Bezdek et al., 1984. FCM: The Fuzzy c-Means Clustering Algorithm. *Computer & Geosciences, 10: 2-3*, 191-203.

---

## Данные для самостоятельной работы

### Фораминиферы маршей Белого моря (Golikova et al. 2020)

![map](images/Golikova_etal_2020_Fig1.png)
---

## Фораминиферы маршей Белого моря

![transect](images/Golikova_etal_2020_fig2.png)
---

## Фораминиферы маршей Белого моря

Plate 1.

1. _Balticammina pseudomacrescens_. 
2. _Ammotium salsum_. 
3. _Jadammina macrescens_. 
4. _Trochammina inflata_. 
5. _Ammobaculites balkwilli?_ 
6. _Miliammina fusca_. 
7. _Ovammina opaca_. 
8. _Elphidium albiumbilicatum_. 
9. _Elphidium williamsoni_.

Scale bar 500 μm.

]

---

## Задание

Проанализируйте данные об относительных обилиях фораминифер в пробах на Белом море.

- Выберите и обоснуйте трансформацию данных и расстояние.

- Постройте ординацию nMDS по относительным обилиям фораминифер:
  - цвет значков --- растение-доминант, 
  - форма значков --- точка сбора.

- Постройте дендрограмму проб по сходству относительных обилий фораминифер.
  - оцените при помощи кофенетической корреляции, какой метод аггрегации лучше,
  
- Постройте визуализацию для методов неиерархической кластеризации

- Опишите получившиеся кластеры при помощи различных параметров:
  - ширина силуэта
  - бутстреп-поддержка ветвлений

---

## Фораминиферы маршей Белого моря

![nMDS](images/Golikova_etal_2020_fig5.png)

---

## Фораминиферы маршей Белого моря

![dendrogram](images/Golikova_etal_2020_fig6.png)