- Объяснить почему для некоторых задач больше подходят многомерные данные
- Объяснить суть понятия “многомерное пространство признаков”
- Представить многомерные данные в виде матриц описания значений признаков для объектов
- Оценить сходство/различие между объектами с помощью специальных коэффициентов
- Описать взаиморасположение объектов в многомерном пространстве признаков с помощью матриц
- Визуализировать взаиморасположение объектов с помощью простейших методов
Вы сможете
Общая характеристика многомерных методов
Почему нужны многомерные методы?
Пусть у нас имеется две группы объектов, у которых мы изучили некий признак. Мы хотим тестировать гипотезу о том, что эти две группы различаются.
Вспомним логику тестирования гипотез.
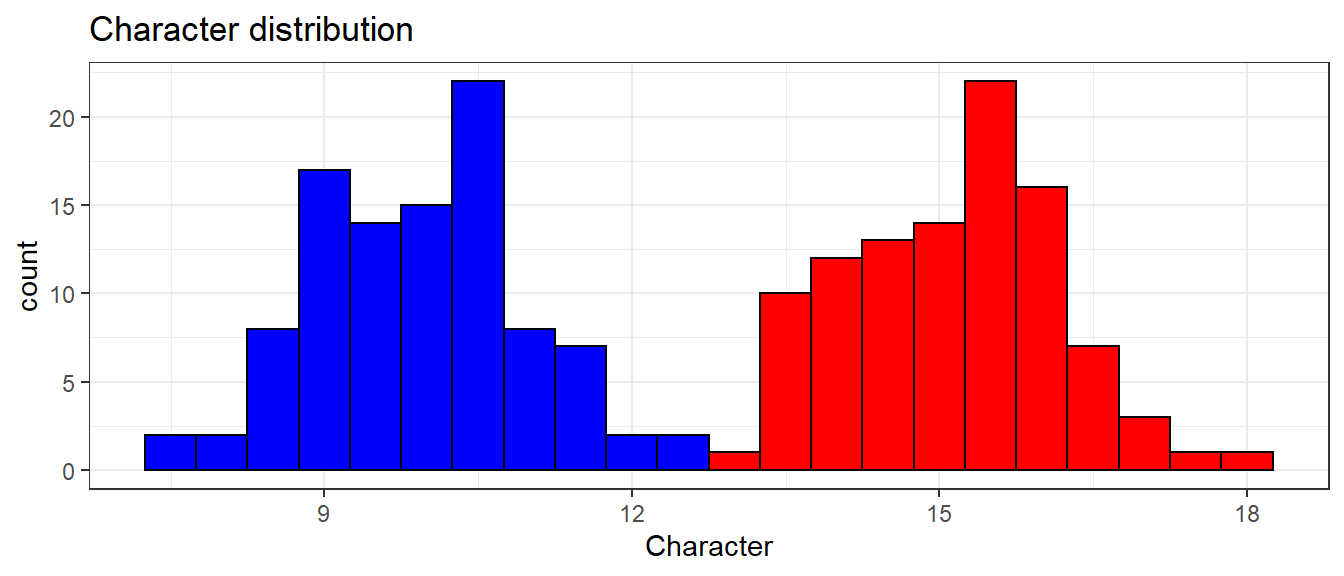
Почему нужны многомерные методы?
Теперь представим, что наш объект, по своей природе, не может быть описан только по одному признаку
- Сообщества (признаки - виды)
- Форма тела (признаки - размеры тех или иных частей)
- Социальная активность животного (признаки - проявление того или иного паттерна)
- Общественное мнение (признаки - ответы на разные вопросы анкет)
- Транскриптом (признаки - транскрипты)
Почему нужны многомерные методы?
Предположим, что объекты характеризуются только двумя признаками
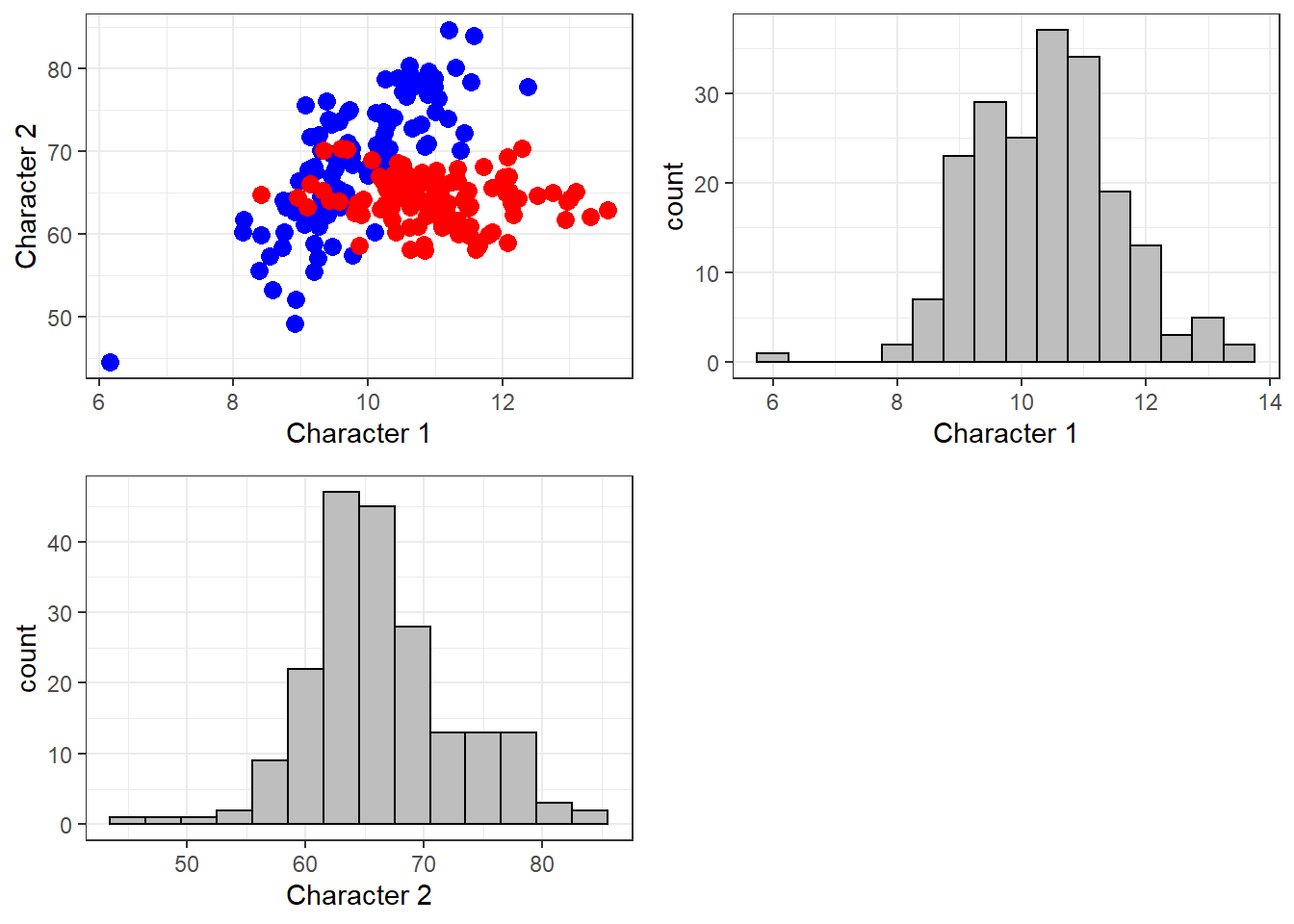
Какие задачи решаются методами могомерной статистики?
- Выявление взаимоотношений (сходства-различия) между объектами (или признаками):
- Классификация (Кластерный анализ)
- Ординация. В том числе картирование пространственно выраженных объектов (nMDS, PCA).
- Тестирование гипотез о различиях между группами объектов (ANOSIM, PERMANOVA).
- Выявление связи между группами признаков (тест Мантела, BIOENV, RDA, CCA).
Признаки и объекты
Данные представляются в виде таблицы (матрицы), где строками являются объекты (Objects), а столбцами признаки (Descriptors).
R и Q анализы
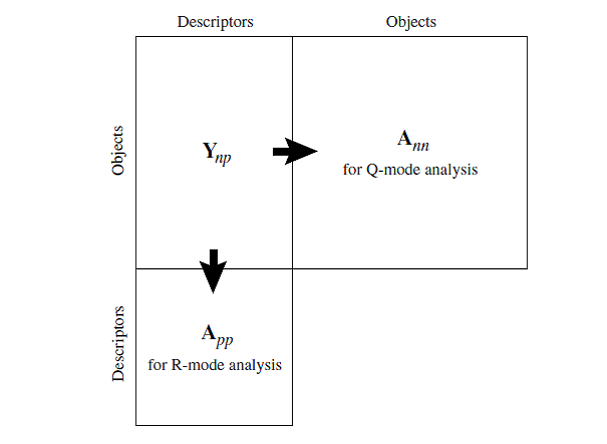
R и Q
- R-анализ: Выясняем взаимоотношения между признаками
- Q-анализ: Выясняем взаимоотношения между объектами
Геометрическая интерпретация Q-анализа
- Признаки - оси
- Объекты - точки
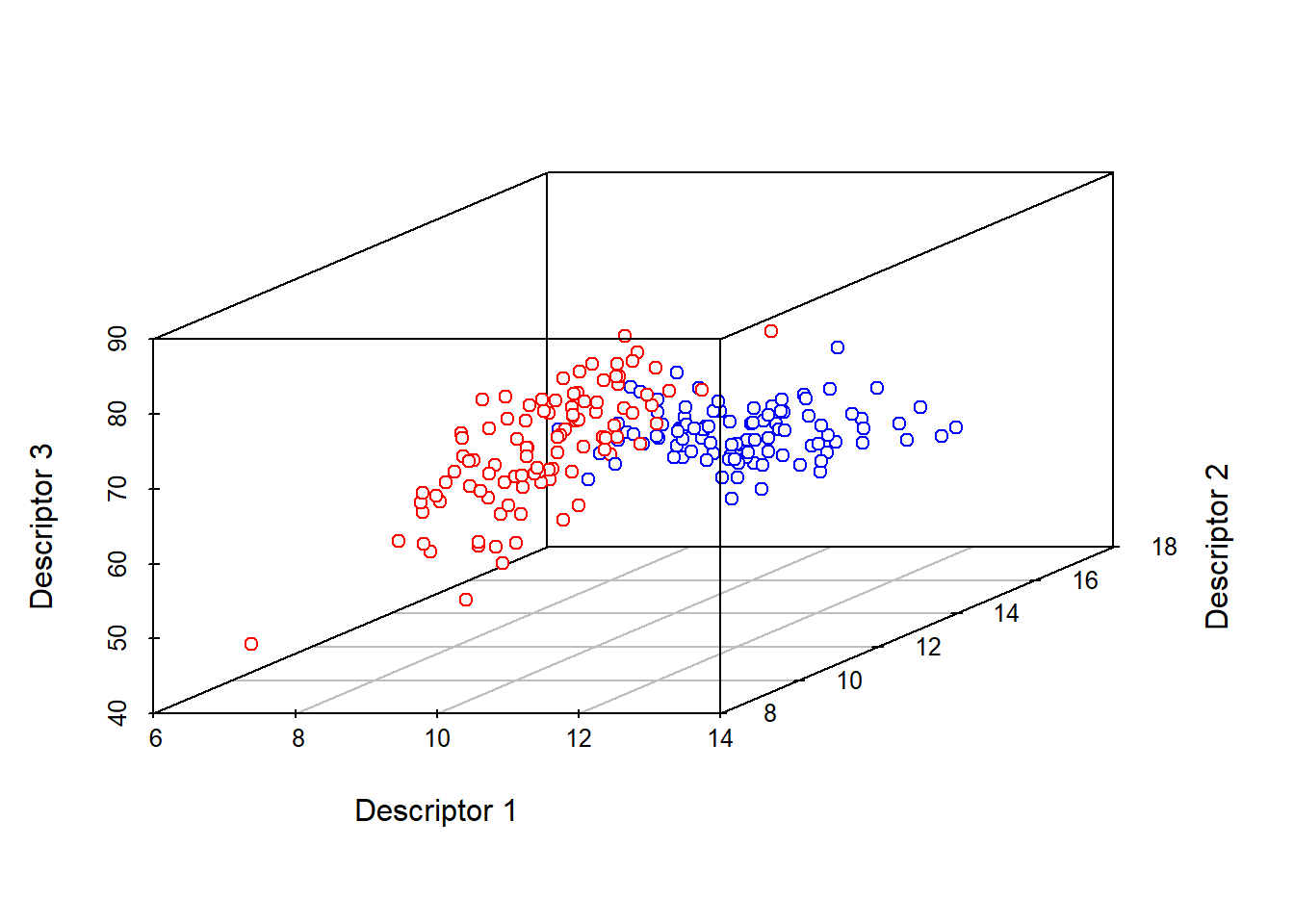
Описание расположения объектов в многомерном пространстве признаков
В большинстве случаев нас интересуют не абсолютные значения координат (признаков), а взаиморасположение точек в многомерном пространстве.
Существует два основных способа описания.
Способ 1. Геометрическое описание (линейная алгебра)
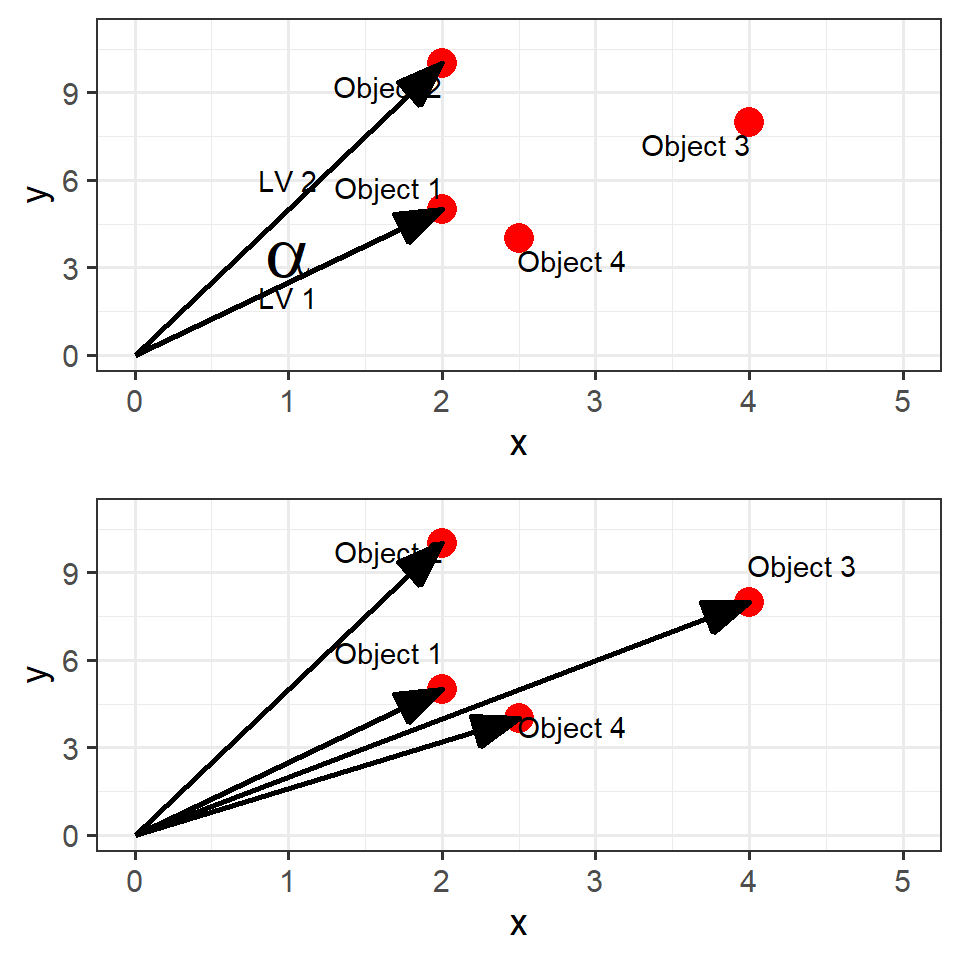
Для описания взаиморасположения точек необходимо иметь два набора данных
Матрицу углов между векторами (косинусов углов)
\[\begin{pmatrix} \alpha_{11} & \alpha_{12} & \cdots & \alpha_{1n} \\ \alpha_{21} & \alpha_{22} & \cdots & \alpha_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ \alpha_{n1} & \alpha_{n2} & \cdots & \alpha_{nn} \end{pmatrix}\]
Ряд длин векторов \[\begin{vmatrix} LV1 \\ LV2 \\ ... \\ LVn \end{vmatrix}\]
Этот способ описания, с разными вариациями, будет применяться в методах PCA, CA, CCA, RDA
Способ 2. Через вычисление матрицы попарных расстояний (Similarity/Dissimilarity matrix)
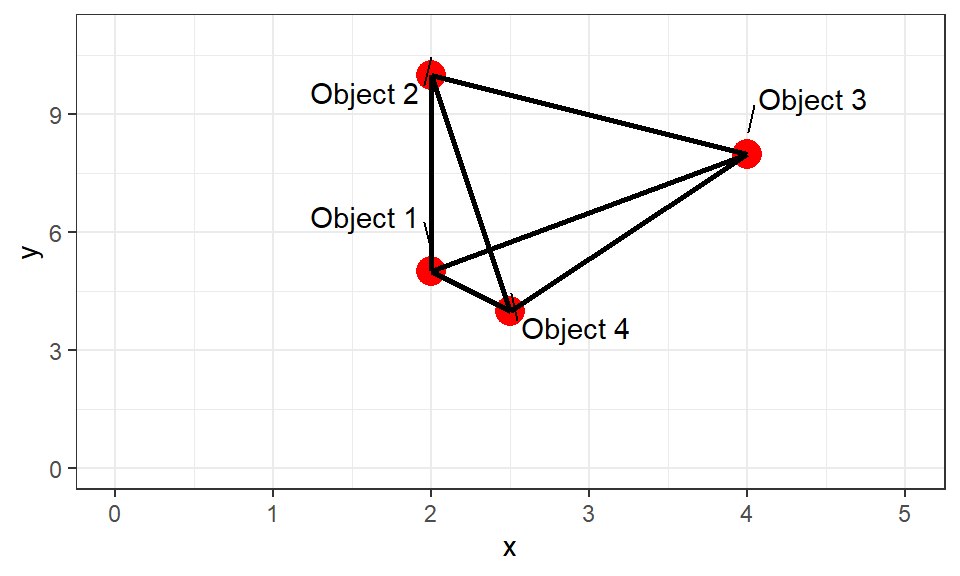
В анализ вовлекается матрица попарных расстояний (сходств) между объектами. Эта матрица однозначно описывает взаиморасположение между объектами.
Этот способ представления взаиморасположения лежит в основе Иерархического кластерного анализа, MDS, теста Мантела, ANOSIM, PERMANOVA, процедуры BIOENV
Простейший многомерный анализ
Простейшая матрица значений признаков
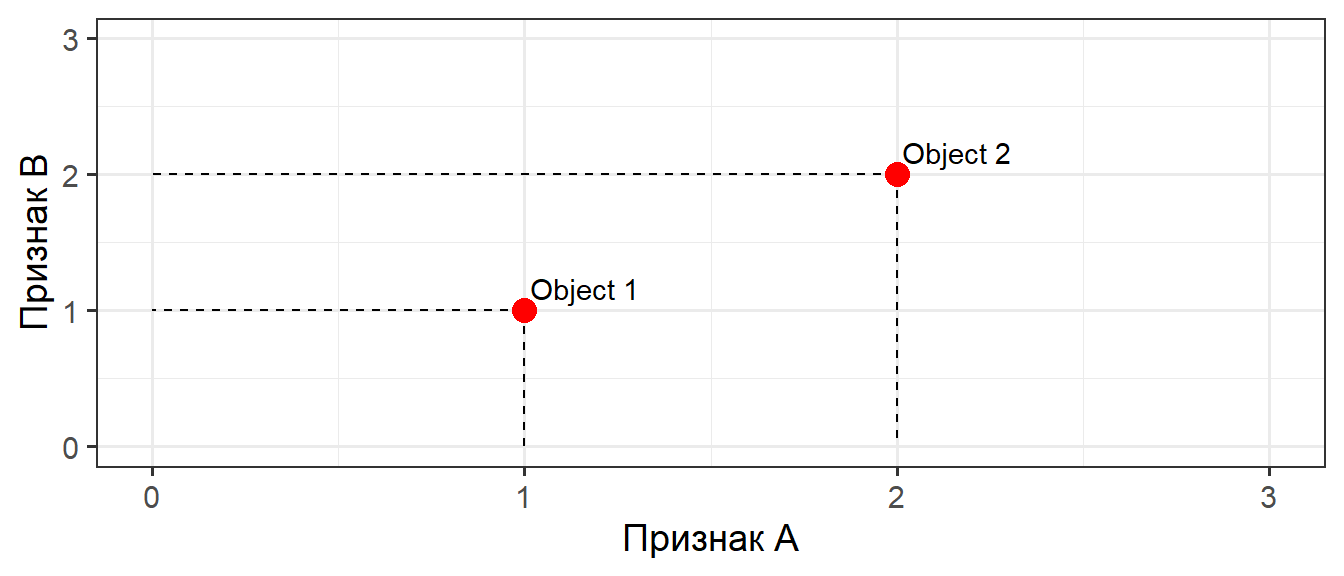
Два объекта и два признака
| Признак А | Признак B | |
|---|---|---|
| Объект 1 | 1 | 1 |
| Объект 2 | 2 | 2 |
Геометрическая интерпретация простейшей матрицы
Евклидово расстояние
Это простейший способ описания расстояния между объектами в пространстве признаков.
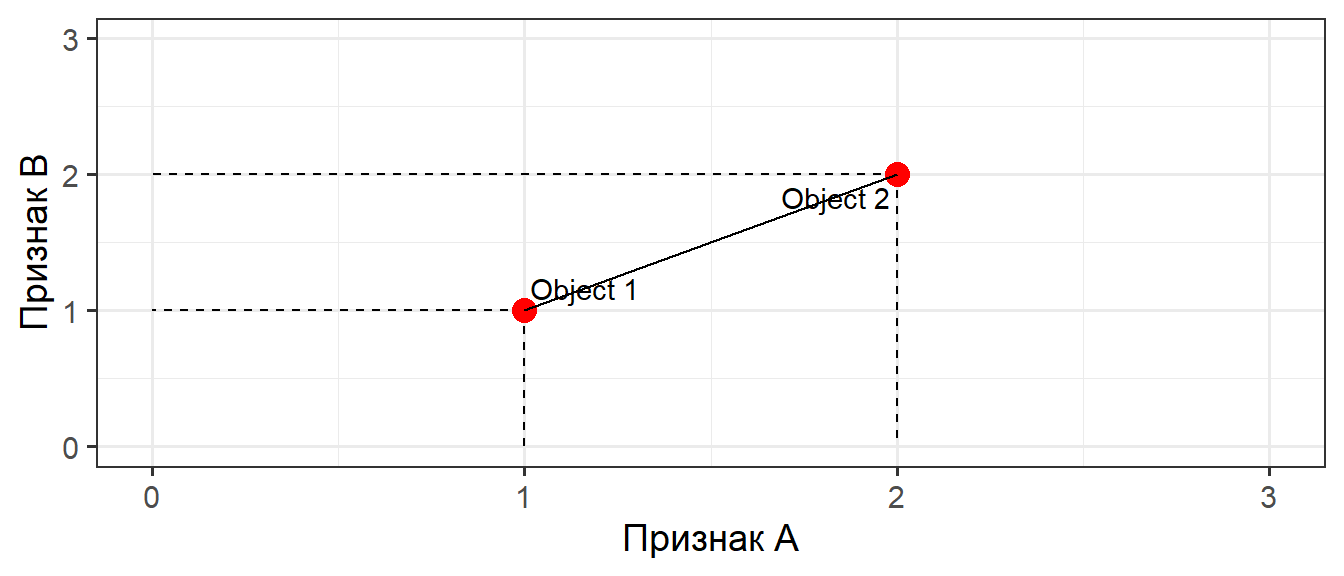
По теореме Пифагора
- \[ D = \sqrt{(A_2 - A_1)^2 + (B_2 - B_1)^2} \]
- Расстояние между объектами выражается просто числом D = 1.414
- At! Эта мера различия между объектами не единственная, и далеко не всегда правильная (об этом далее).
Усложняем задачу: объектов становится больше двух
| Объект | Признак А | Признак B |
|---|---|---|
| Object 1 | 2.0 | 5 |
| Object 2 | 2.0 | 10 |
| Object 3 | 4.0 | 8 |
| Object 4 | 2.5 | 4 |
Геометрическая интерпретация
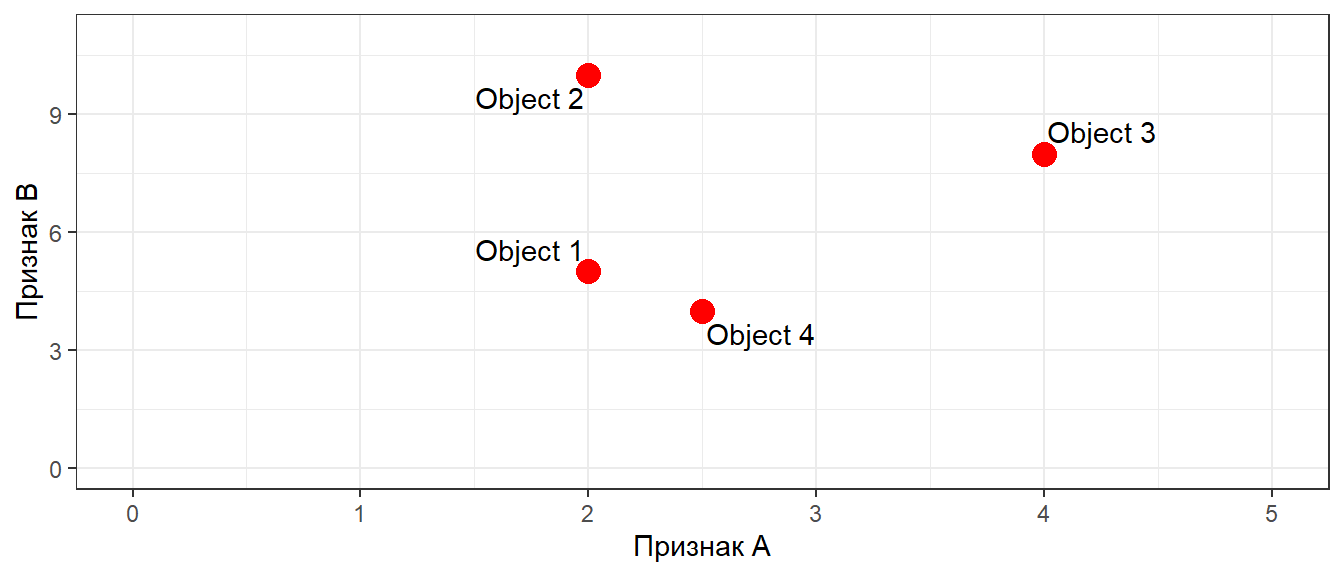
Матрица расстояний (Similarity/Dissimilarity matrix)
Когда объектов больше двух, то расстояния между объектами можно выразить матрицей расстояний.
## 1 2 3 4 ## 1 0.0 5.0 3.6 1.1 ## 2 5.0 0.0 2.8 6.0 ## 3 3.6 2.8 0.0 4.3 ## 4 1.1 6.0 4.3 0.0
Охарактеризуйте эту матрицу
- Квадратная матрица
- Симметричная матрица
Усложняем задачу: признаков становится больше двух
| Объект | Признак А | Признак B | Признак С | Признак D |
|---|---|---|---|---|
| Object 1 | 2.0 | 5 | 100 | 0.10 |
| Object 2 | 2.0 | 10 | 258 | 0.01 |
| Object 3 | 4.0 | 8 | 122 | 0.09 |
| Object 4 | 2.5 | 4 | 10000 | 0.15 |
Геометрическая интрепретация
Облако точек в n-мерном пространстве значений признаков.
At! Не пытайтесь представить n-мерный объект… Просто работайте с ним.
- Warning

Эвклидово расстояние в n-мерном пространстве
\[D = \sqrt{\sum(x_{i,j} - x_{i,k})^2}\]
В n-мерном пространстве соблюдаются те же законы, что и на плоскости.
Три способа изображения матрицы расстояний
## 1 2 3 4 ## 1 0.0 158.1 22.3 9900.0 ## 2 158.1 0.0 136.0 9742.0 ## 3 22.3 136.0 0.0 9878.0 ## 4 9900.0 9742.0 9878.0 0.0
## 1 2 3 4 ## 1 0.0 ## 2 158.1 0.0 ## 3 22.3 136.0 0.0 ## 4 9900.0 9742.0 9878.0 0.0
## 1 2 3 ## 2 158.1 ## 3 22.3 136.0 ## 4 9900.0 9742.0 9878.0
Количество значимых чисел в треугольной матрице:
\[N = \frac{n^2 - n}{2}\]
Матрица расстояний в развернутом виде (Unfolded dissimilarity matrix)
## 1 2 3 ## 2 158.1 ## 3 22.3 136.0 ## 4 9900.0 9742.0 9878.0
## [1] 158.1 22.3 9900.0 136.0 9742.0 9878.0
Результаты простейшего могомерного анализа
Исходная матрица признаков
| Объект | Признак А | Признак B | Признак С | Признак D |
|---|---|---|---|---|
| Object 1 | 2.0 | 5 | 100 | 0.10 |
| Object 2 | 2.0 | 10 | 258 | 0.01 |
| Object 3 | 4.0 | 8 | 122 | 0.09 |
| Object 4 | 2.5 | 4 | 10000 | 0.15 |
Матрица расстояний
## 1 2 3 ## 2 158.1 ## 3 22.3 136.0 ## 4 9900.0 9742.0 9878.0
- Какие объекты наиболее похожи друг на друга?
- Какие объекты наиболее различны?
- В чем проблема данного анализа?
Простейший анализ реальных многомерных данных
Пример: Сообщества бентоса акватории Долгой губы (о. Б. Соловецкий, Белое море)
В этом примере используется сокращенный набор данных о бентосе Долгой губы (Нинбург, 1990; Хайтов и др., 2013) — только численность наиболее обильных видов на 68 станциях.
dolg_abundance.txt— данные об обилии 25 видовdolg_hydrology.txt— данные о 4 гидрологических характеристиках: глубина, Температура придонной воды, Соленость, Степень гидратации грунта
Читаем данные
abund <- read.table("data/dolg_abundance.txt", skip = 1, header = TRUE, sep = ";")
hydrol <- read.table("data/dolg_hydrology.txt", skip = 1, header = TRUE, sep = ";")
Вопрос для многомерного анализа
Существуют ли группировки описаний, сходных по населению?
Задание: Нарисуйте на бумаге как, по вашему мнению, должны располагаться объекты (описания-станции) в n-мерном пространстве признаков, если существует две группировки.
Подготовка данных для анализа
Переменные могут быть измерены в разных шкалах
- численность, биомасса и проективное покрытие разных организмов
- температура воды, соленость и концентрация биогенов
- Размеры частей тела, количество частей тела, площадь частей тела
Для таких случаев необходима стандартизация величин. Этот прием будет постоянно применяться при многомерных анализах, основанных на матричной алгебре.
\[x_{stand} = \frac{x_i - \bar{x}}{\sigma_x}\]
- Вопрос: Какими свойствами обладают стандартизованные величины?
- Среднее значение равно нулю.
- Среднеквадратичное отклонение равно единице.
Подготовка данных для анализа
В ряде случаев (особенно в экологических исследованиях) необходимо перевести абсолютные значения в относительные (доли от суммы или от максимума)
\[x_{rel} = \frac{x_i}{\sum x_i} \times 100 \%\]
\[x_{rel} = \frac{x_i}{max(x_i)} \times 100 \%\]
Подготовка данных для анализа
Часто возникает ситуация, когда один признак (или несколько признаков) имеет существенно более высокие абсолютные значения, чем все остальные, или варьирует в более широких пределах, чем остальные признаки.
В такой ситуации необходима трансформация , которая “уравнивает” силу влияния признаков.
По силе эффекта трансформирующие функции распределяются так:
Отсутствие трансформации \(\Rightarrow\) Квадратный корень \(\Rightarrow\) Корень четвертой степени \(\Rightarrow\) Логарифм \(log(x_i +1)\) \(\Rightarrow\) Присутствие отсутствие (1, 0)
Задание:
На основе датасета, содержащего данные по обилию видов, создайте матрицу, содержащую относительные величины (доли обилия каждого вида в общем обилии организмов на данной станции)
Hint: Воспользуйтесь функцией apply()
Решение
total <- apply(abund[, -1], MARGIN = 1,FUN = sum) abund_rel <- abund[, -1] / total head(abund_rel[,1:3])
## Eteone_longa Nemertini Harmothoe_imbricata ## 1 0.0000 0.00772 0.0232 ## 2 0.0000 0.00000 0.0000 ## 3 0.0000 0.00000 0.0000 ## 4 0.0000 0.00000 0.0000 ## 5 0.0000 0.02857 0.0000 ## 6 0.0143 0.01429 0.0000
Знакомимся с пакетом vegan (Oksanen et al., 2015)
library (vegan)
- Пакет
veganпозволяет проводить много типов многомерных анализов (но не все!). - Ориентирован на экологические данные, отсюда много экологических терминов (признаки – “species”, объекты – “sites”)
- Исчерпывающее описание методов, реализованных в
vegan, дается в “Numerical ecology” (Legendre & Legendre, 2012) - Альтернатива – пакет
ade4
Подготовка данных в пакете vegan
Относительные величины
abund_rel <- decostand(abund[,-1], method = "total", MARGIN = 1) head(abund_rel[, 1:3])
## Eteone_longa Nemertini Harmothoe_imbricata ## 1 0.0000 0.00772 0.0232 ## 2 0.0000 0.00000 0.0000 ## 3 0.0000 0.00000 0.0000 ## 4 0.0000 0.00000 0.0000 ## 5 0.0000 0.02857 0.0000 ## 6 0.0143 0.01429 0.0000
Задание
С помощью пакета vegan создайте еще два датасета:
abund_stand– Стандартизованные величины обилий видовabund_log– Логарифмированные величины обилий видов
Решение: стандартизация в vegan
abund_stand <- decostand(abund[,-1], method = "standardize", MARGIN = 2) head(abund_stand[, 1:3])
## Eteone_longa Nemertini Harmothoe_imbricata ## 1 -0.329 0.6878 2.783 ## 2 -0.329 -0.5594 -0.508 ## 3 -0.329 -0.5594 -0.508 ## 4 -0.329 -0.5594 -0.508 ## 5 -0.329 0.6878 -0.508 ## 6 0.118 0.0642 -0.508
Решение: log-трансформация в vegan
abund_log <- decostand(abund[,-1], method = "log", MARGIN = 2) head(abund_log[, 1:3])
## Eteone_longa Nemertini Harmothoe_imbricata ## 1 0.00 6.32 7.91 ## 2 0.00 0.00 0.00 ## 3 0.00 0.00 0.00 ## 4 0.00 0.00 0.00 ## 5 0.00 6.32 0.00 ## 6 5.32 5.32 0.00
Матрицы расстояний в пакете vegan
dist_init <- vegdist(abund[,-1], method = "euclidean") dist_stand <- vegdist(abund_stand, method = "euclidean") dist_log <- vegdist(abund_log, method = "euclidean") dist_rel <- vegdist(abund_rel, method = "euclidean")
Существуют ли группировки в n-мерном облаке точек?
Самый простой анализ - частотное распределение расстояний между объектами.
Позволяет понять есть ли сгущения в облаке точек в n-мерном пространстве признаков.
Задание: Создайте вектор, соответствующий развернутой (unfolded) матрице эвклидовых расстояний, основанной на относительных обилиях видов, и постройте частотную гистограмму для этого вектора.
Решение
disatances <- data.frame(Init = as.numeric(dist_init),
Stand = as.numeric(dist_stand),
Log = as.numeric(dist_log),
Rel = as.numeric(dist_rel))
Pl_hist <- ggplot(disatances) + geom_histogram()
Pl_init <- Pl_hist + aes(x = Init) + ggtitle("Исходные данные") + labs(x = "Евклидово расстояние")
Pl_stand <- Pl_hist + aes(x = Stand) + ggtitle("Стандартизация") + labs(x = "Евклидово расстояние")
Pl_log <- Pl_hist + aes(x = Log) + ggtitle("Логарифмирование")+ labs(x = "Евклидово расстояние")
Pl_rel <- Pl_hist + aes(x = Rel) + ggtitle("Относительные величины")+ labs(x = "Евклидово расстояние")
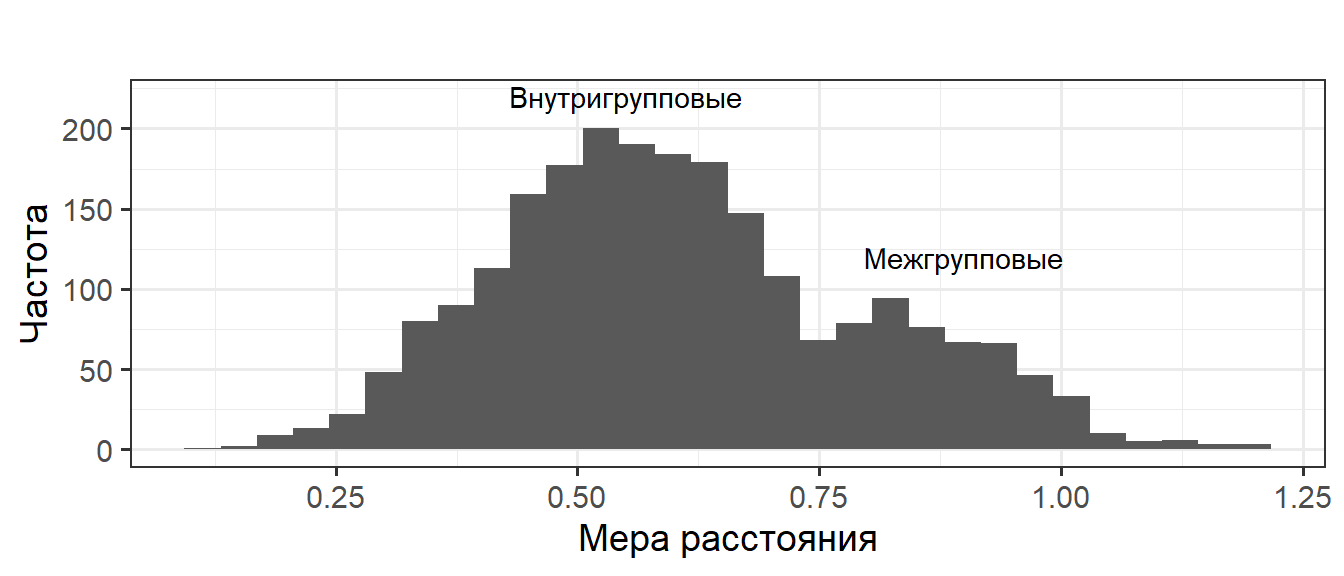
Существуют ли группировки?
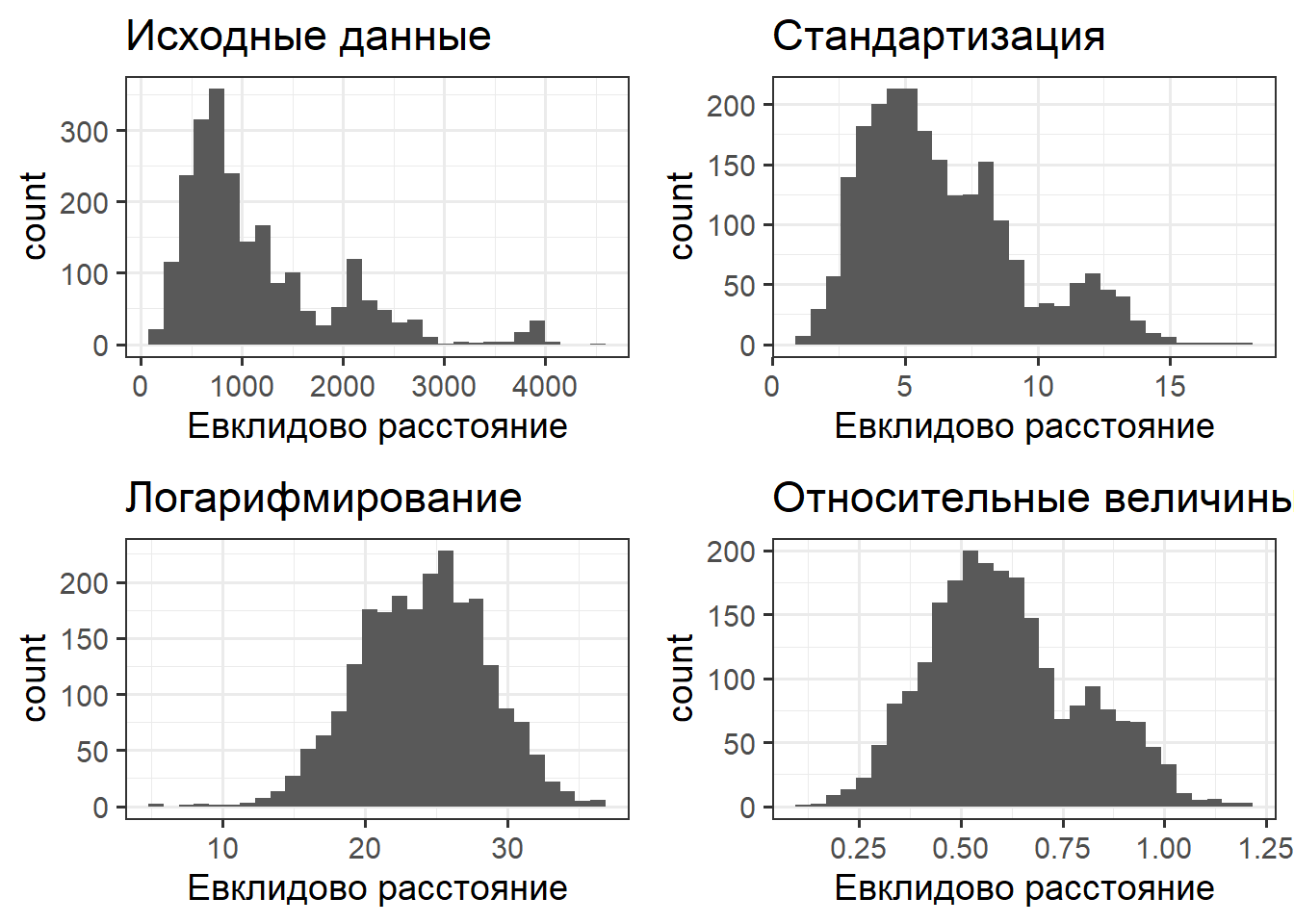
Структура облака точек
Если в n-мерном облаке точек присутствуют несколько “сгущений”, то расстояния между объектами делятся на внутригрупповые (пик в области малых значений расстояний) и межгрупповые (пик в области высоких значений)
Меры сходства и различия между объектами (Resemblance coefficients)
От того в чем измерено различие многое зависит
Мы уже знаем, что от способа выражения признаков очень многое зависит.
Однако еще сильнее анализ зависит от того с помощью какой величины (Resemblance coefficients) описывается степень различия между объектам.
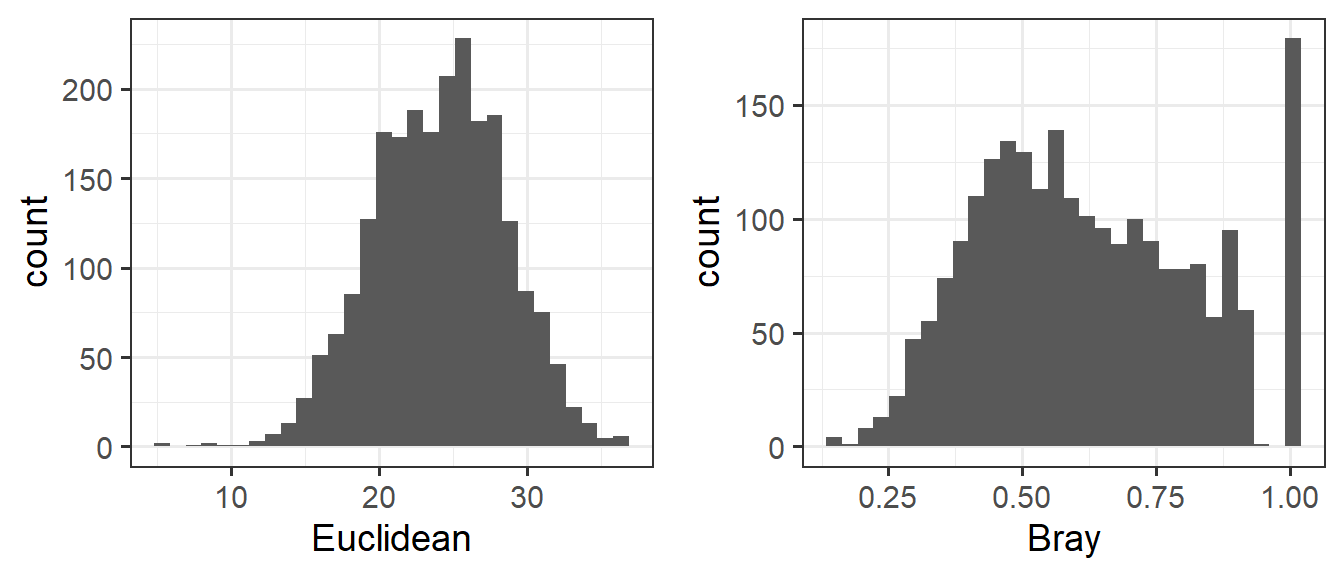
Задание: 1. На базе датасета abund_log, используя функцию vegdist() рассчитайте матрицу различий между объектами (dist_eucl), основанную на евклидовом расстоянии.
На том же датасете постройте матрицу различий (
dist_bray), основанную на методе, называемом ‘bray’.Разверните обе матрицы в векторы.
Постройте для этих векторов частотные диаграммы.
Решение
dist_eucl <- vegdist(abund_log, method = "euclidean")
dist_bray <- vegdist(abund_log, method = "bray")
dists <- data.frame(Euclidean = as.numeric(dist_eucl),
Bray = as.numeric(dist_bray))
Pl_hist <- ggplot(dists) + geom_histogram()
Pl_eucl <- Pl_hist + aes(x = Euclidean)
Pl_bray <- Pl_hist + aes(x = Bray)
Решение
grid.arrange(Pl_eucl, Pl_bray, ncol = 2)
Сходства и различия
Сходство (S) достигает максимума, когда объекты обладают идентичными признаками, различиe (D), наоборот - достигает минимума.
Обычно (но не всегда) коэффициенты сходства распределены от 0 до 1.
Тогда \(D = 1 - S\), или \(D = \sqrt{1 - S}\), или \(D = \sqrt{1-S^2}\).
Показатели можно нормировать. \(D_{norm} = \frac{D}{D_{max}}\), или \(D_{norm} = \frac{D - D_{min}}{D_{max} - D_{min}}\).
В большинстве случаев нас будут интересовать меры различия между объектами
Проблема двойных нулей (Double zeros probem)
## D1 D2 D3 D4 D5 D6 D7 D8 D9 D10 ## Object1 0 0 0 0 0 0 0 2 2 1 ## Object2 0 0 0 0 0 4 5 0 0 1
О чем говорит то, что признаки D1, D2, D3, D4, D5 не были отмечены у двух объектов?
- Вариант 1. Это ничего не означает. Признаки D1, D2, D3, D4, D5 можно не учитывать при сравнении объектов 1 и 2.
- Вариант 2. Отсутствие признака - дополнительное сходство между объектами. Сходство между объектами 1 и 2 повышается так как у них нет признаков D1, D2, D3, D4, D5, которые возможно есть у других объектов.
- От выбора одного из двух вариантов зависит какой коэффициент использовать в анализе.
Два типа коэффициентов
Меры различия не учитывающие двойные нули. Эти коэффициенты не изменяются если в данные будут добавлены двойные нули (например, при увеличении количества описанных объектов).
Примеры:
- Евклидово расстояние
- расстояние по Манхеттену.
Меры различия учитывающие двойные нули. Эти коэффициенты изменяются при появлении двойных нулей. Сходство возрастает за счет того, что отсутствие признака считается тоже сходством.
Пример:
- Коэффициенты корреляции.
Меры расстояния, или метрики
Свойства:
- Если \(a = b\), то \(D(a, b) = 0\)
- Симметричность \(D(a, b) = D(b, a)\)
- Справедливо неравенство треугольника \(D(a,b) + D(b,c) \geq D(a,c)\)
Важно: метрики неадекватно оценивают степень различия при большом количестве нулей.Очень чувствительны к выбросам.
Наиболее популярные меры расстояния (метрики)
Нестандартизованные
- Евклидово расстояние:
\[D = \sqrt{\sum(x_{i,j} - x_{i,k})^2}\]
- Расстояние по Манхеттену (Manhattan metric, taxicab metric, city-block metric):
\[D = \sum \mid x_{i,j} - x_{i,k} \mid\]
Стандартизованные
Удобнее так как признаки могут быть измерены в разных шкалах
- Расстояние по Канберре (Canberra metric):
\(D = \frac{1} {p} \sum \frac {\mid x_{i,j} - x_{i,k} \mid} {x_{i,j}+ x_{i,k}}\)
- Расстояние \(\chi^2\)
\(\chi^2 = \sqrt{ \sum {\frac{1}{c_i}} (x_{i,j} - x_{i,k})^2}\)
- Евклидово расстояние, вычисленное по относительным величинам.
Полуметрики
Некоторые меры расстояния не отвечают требованиям метрик
Расстояние Махаланобиса
\[D = \sqrt{(x - y) Cov^{-1}(x - y)^T}\]
\(x\) и \(y\) - Векторы координат точек \(a\) и \(b\) в пространстве признаков. \(Cov\) - Матрица ковариации
Свойства полуметрик:
- Если \(a = b\), то \(D(a, b) = 0\)
- Симметричность \(D(a, b) = D(b, a)\)
- НО! Не справедливо неравенство треугольника \(D(a,b) + D(b,c) \geq D(a,c)\) (из-за наличия ковариации между векторами)
Неметрические коэффициенты различия
- Корреляция Браве-Пирсона: \[ R = \frac {cov(X, Y)}{\sqrt{\sigma_x^2\sigma_y^2}} \]
Коэффициент Браве-Пирсона варьирует от -1 до 1.
Обычно используется в R анализе
- Коэффициент Брея-Куртиса (Bray-Curtis dissimilarity): \[D = \frac{\sum \mid x_{i,j} - x_{i,k} \mid} {\sum x_{i,j} + \sum x_{i,k}}\]
Это самый распространенный коэффициент в экологии.
Коэффициенты для бинарных данных
В основе лежит четырехпольная таблица
\[\begin{vmatrix} \, & + & - \\ + & a & b \\ - & c & d \end{vmatrix}\]
- a - сходство объектов по наличию признака
- b - различие
- c - различие
- d - сходство по отсутствию признака
Коэффициенты для бинарных данных
- Доля несовпадений:
\[D = \frac{b+c}{a+b+c}\]
- Коэффициент Жаккара:
\[S = \frac{a}{a+b+c}\]
- Коэффициент Сёренсена:
\[S = \frac{2a}{2a + b + c}\]
Коэффициенты для бинарных данных
- \(\phi\)-корреляция Пирсона
\[\phi = \frac{ad-bc}{(a+b)(c+d)(a+c)(b+d)}\]
Используется в R-анализе
Коэффициент Говера
Обобщенный коэффициент, который применяется для случаев, когда одни признаки объекта описаны, как количественные величины, а другие - как бинарные данные (или даже качественные данные).
\[ D = \frac{1}{p} \frac{\sum W_i\dfrac{\mid x_{i,j} - x_{i,k} \mid}{\max x_{i,j} - \min x_{i,k}}}{\sum W_i}\]
\(W_i=0\) Если отсутствует информация o \(x_{i,j}\) и/или \(x_{i,k}\) отсутствует
\(W_i=1\) Если присутствует информация как о \(x_{i,j}\) так и о \(x_{i,k}\)
Отчего зависит выбор коэффициента?
- От природы материала (признаки могут иметь количественную, бинарную и качественную оценку).
- От характера тестируемой гипотезы (какой аспект природы сходства-различия хочет выразить автор).
- В экологии: от того, насколько мы хотим учитывать вклад редких и малочисленных видов.
- От взглядов исследователя на природу сходства/различия между объектами.
- От типа анализа (R или Q)
Многие показатели взаимосвязаны и, часто, взаимозаменяемы
Ординация – основной метод описания многомерных данных
Многомерные объекты, их свойства и внешние факторы
| Элемент анализа | (син)экология | морфология | молекулярная биология |
|---|---|---|---|
| Объекты | площадки / пробы | особи / клетки и т.п. | особи / клетки и т.п. |
| Собственные свойства объектов | численность / биомасса особей разных видов | измерения, свойства | интенсивность экспрессии гена/пептида |
| Внешние факторы | свойства среды | свойства среды / особей / клеток | свойства среды / особей / клеток |
По аналогии с одномерными линейными моделями
- Объекты – Измерения
- Свойства объектов – Зависимая переменная
- Внешние факторы – Предикторы
Ординация
Ординация (лат. ordinatio — расположение в порядке) — это упорядочивание объектов вдоль некоторых осей, определяющих варьирование свойств этих объектов.
Если у объектов всего два свойства, то ординация имеет вид облака точек в двух осях.
Аналогия ординации с одномерными методами – просто числовой ряд.
Ординация в сокращенном пространстве признаков (Оrdination in reduced space)
Если признаков становится больше двух, то визуализация взаиморасположения объектов в n-мерном пространстве признаков становится невозможной. Для этого применяют разные способы получения “образа” n-мерного облака:
Старинные методы:
- Висконсинская полярная ординация (Bray and Curtis, 1957)
Современные методы:
- Метрическое многомерное шкалирование (MDS)
- Неметричекое многомерное шкалирование (nMDS)
- Метод главных компонент (PCA)
- Корреспондентный анализ (CA)
Висконсинская полярная ординация
Это простейший прием ординации в сокращенном пространстве
Шаг 1. Подготовка данных для анализа.
Логарифмирование мы провели ранее
row.names(abund_rel) <- abund$Station
Висконсинская полярная ординация
Шаг 2. Вычисление матрицы сходства/различия между объектами.
Из дидактических соображений возьмем матрицу Евклидовых расстояний.
library(vegan) E_dist <- vegdist(abund_log, method = "euclidean")
Висконсинская полярная ординация
Шаг 3. Найдем наиболее различающиеся объекты (максимальное Евклидово расстояние между ними).
## i Object_j Object_k Distance ## 1991 1991 44 57 36.6
Эти два объекта и задают ось, вдоль которой будет производиться ординация.
Висконсинская полярная ординация
Шаг 4. Координаты каждого из объектов на этой оси могут быть найдены, согласно правилам треугольника
Возьмем любую другую точку, например “S2”
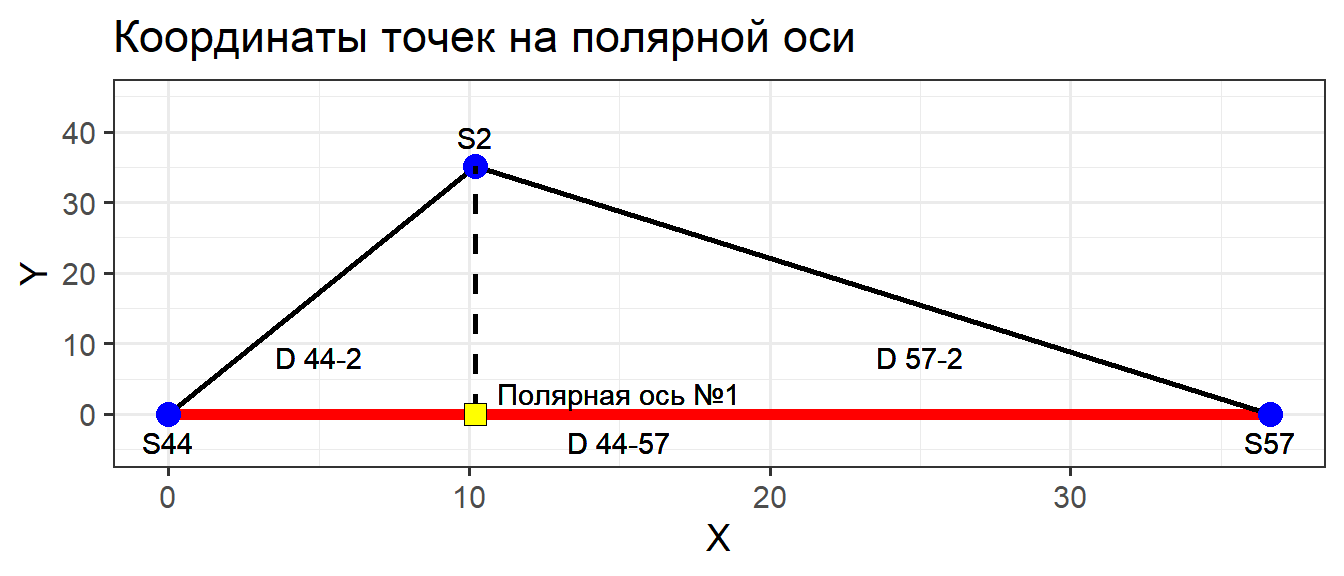
Висконсинская полярная ординация
Шаг 5. Вычисляем координаты на полярной оси для каждого объекта.
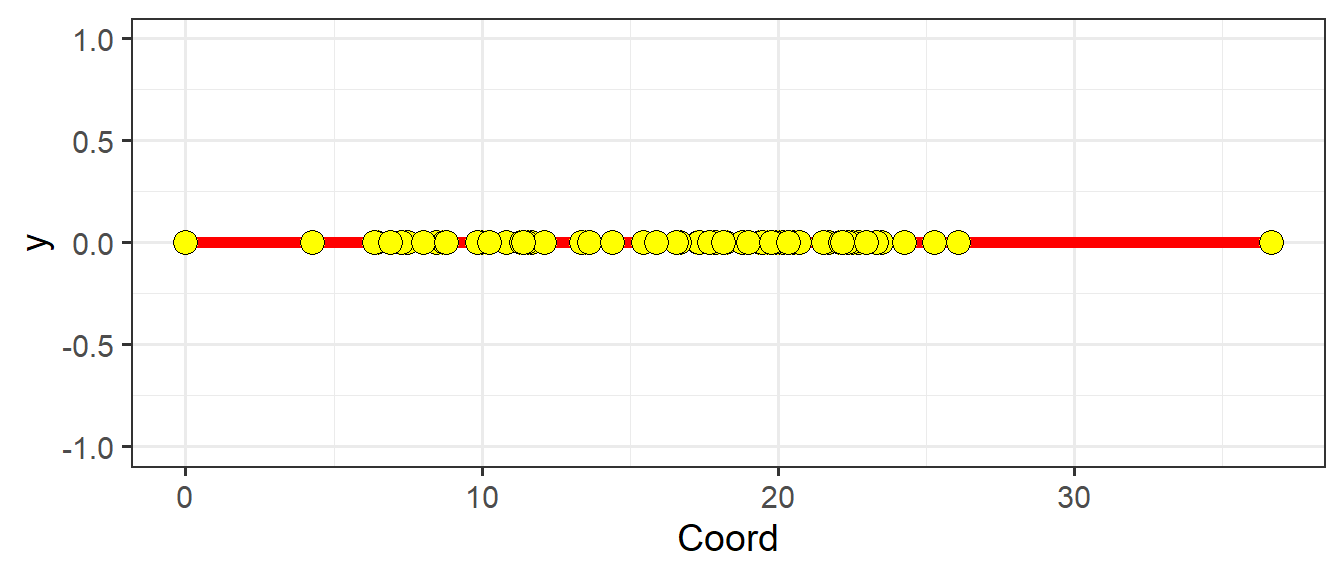
Висконсинская полярная ординация
Шаг 6. При необходимости, находим следующую пару наиболее несходных объектов и вычисляем координаты для каждой точки на новой оси.
At! Одновременное изображение информации об обеих полярных осях на одной диаграмме невозможно!
Мы не знаем как взаимосвязаны эти оси. Они могут быть неортогональны.
Интерпретация результатов ординации
Сама по себе ординация - это лишь визуализация структуры многомерных данных.
Исследователю важно объяснить, с какими внешними факторами связана наблюдаемая ординация.
Пример: Структура сообщества и градиент температуры
С помощью Висконсинской полярной ординации мы получили градиент точек на полярной оси.
Этот градиент связан с внешним фактором - температурой.
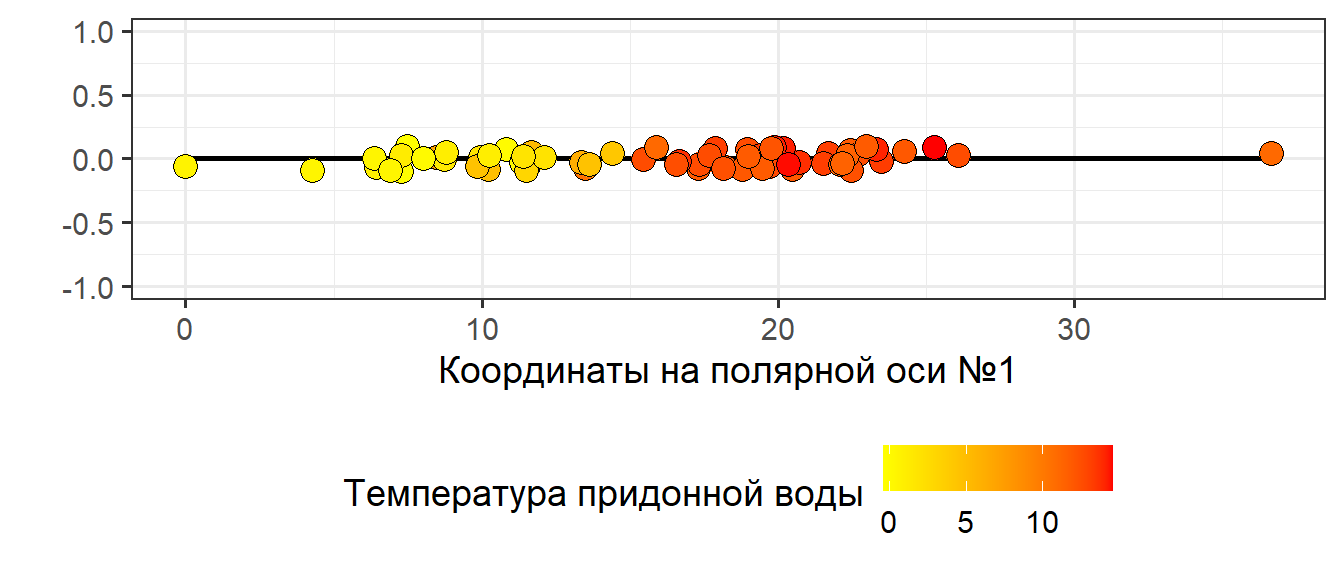
Две схемы интерпретации
Методы интерпретации многомерных данных делят на две большие группы (ter Braak, 1987; Legendre & Legendre, 2014):
Непрямая интерпретация (indirect gradient analysis, indirect comparison)
Прямая интерпретация (direct gradient analysis, direct comparison)
Методы непрямой интерпретации
Синоним – неограниченная ординация (unconstrained ordination).
Мы строим ординацию (или используем иной тип визуализации), основанную на свойствах самих объектов, далее пытаемся связать эту ординацию с внешними факторами.
Методы неограниченной ординации:
- Висконсинская полярная ординация
- неметрическое многомерное шкалирование (non-Metric Multidimensional Scaling, nMDS)
- анализ главных компонент (Principal Component Analysis, PCA)
- корреспондентный анализ (Correspondence Analysis, CA).
После построения ординации на нее накладывают информацию о внешних факторах:
Простейший способ: Построить точечные диаграммы, отражающие связь координат осей ординации с той или иной внешней переменной.
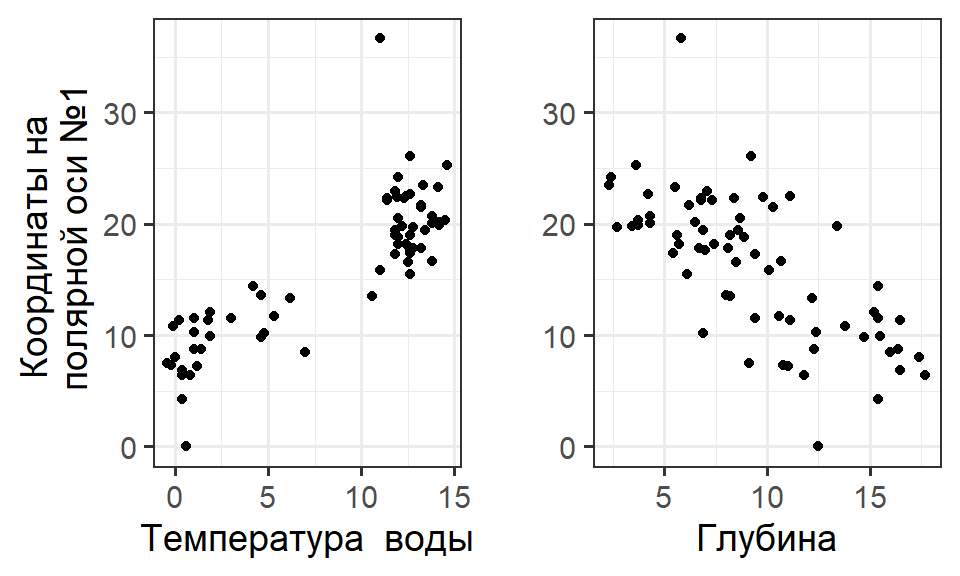
Задание
Вычислите значения координат полярной ординации, основанной на относительных обилиях видов (abund_rel) и постройте точечную диаграмму, отражающую связь этой ординации с глубиной, температурой? соленостью и обводненностью грунта.
Решение
New_coord2 <- polarord(abund_rel) Pl_1 <- qplot(hydrol$Temp, New_coord2$Coord) + labs(x = "Температура", y = "Координаты ординации") Pl_2 <- qplot(hydrol$Depth, New_coord2$Coord) + labs(x = "Глубина", y = "Координаты ординации") Pl_3 <- qplot(hydrol$Sal, New_coord2$Coord) + labs(x = "Соленость", y = "Координаты ординации") Pl_4 <- qplot(hydrol$Water_content, New_coord2$Coord) + labs(x = "Обводненность", y = "Координаты ординации")
Решение
grid.arrange(Pl_1, Pl_2, Pl_3, Pl_4, ncol = 2)
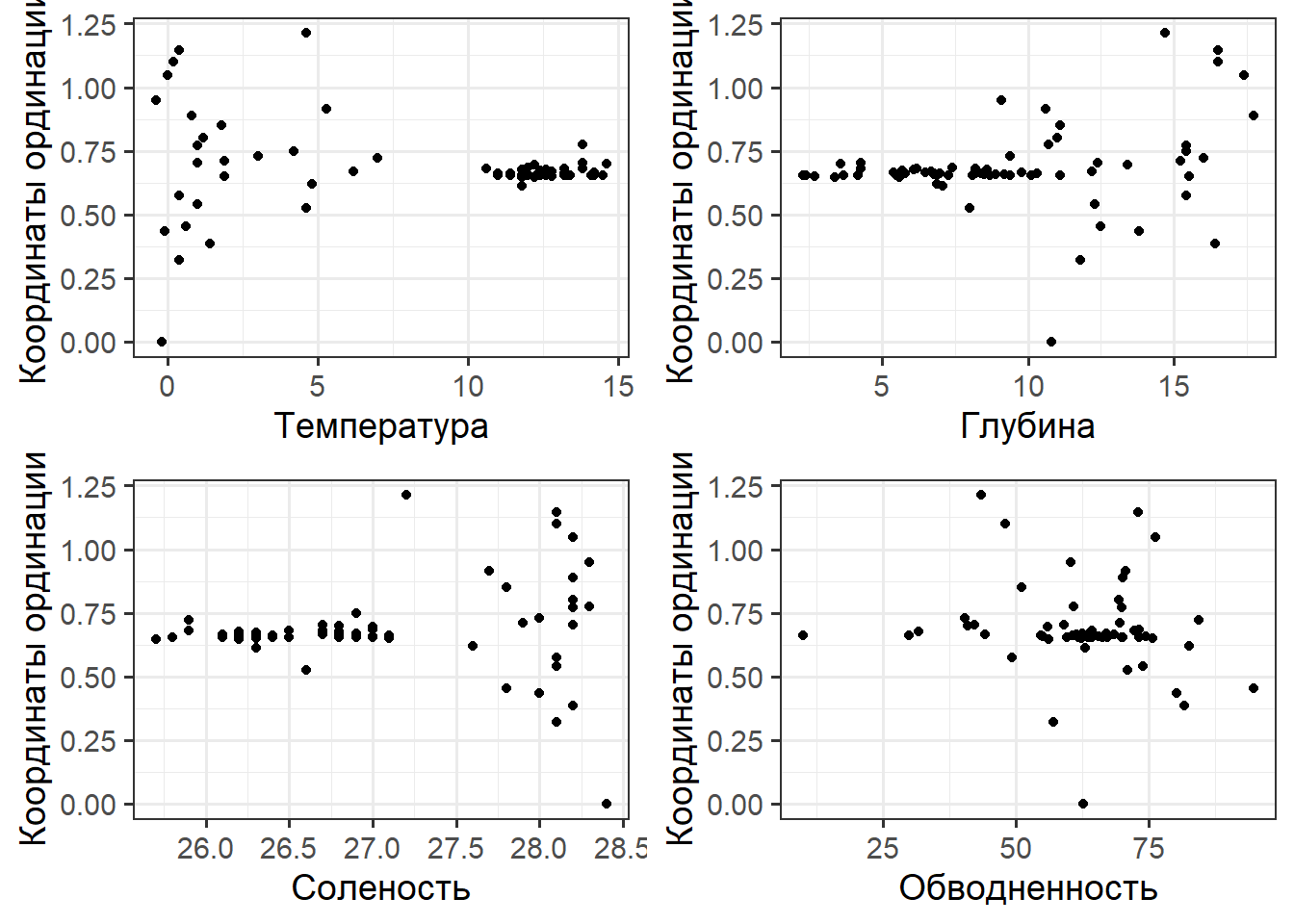
Методы прямой интерпретации
Синоним – ограниченная ординация (constrained ordination).
Для построения ординации в один анализ включаются и свойства объектов и внешние факторы. Итоговая ординация отражает результат взаимосвязи свойств объектов с внешними факторами.
Методы прямой ординации позволяют тестировать гипотезы о влиянии различных внешних переменных на свойства многомерных объектов:
Методы ограниченной ординации:
- анализ избыточности (Redundancy Analysis, RDA)
- канонический корреспондентный анализ (Canonical Correspondence Analysis, CCA).
Summary
- Существует два подхода к анализу многомерных данных:
- подход, основанный на линейной алгебре,
- подход, основанный на исследовании матриц сходства/различия между объектами.
- Выбор коэффициентов сходств/различия - непростая задача, решение которой зависит от структуры материала и поставленных задач. Разные коэффициенты потенциально могут давать разные результаты.
- Получить важную информацию о взаиморасположении объектов можно с помощью некоторых простейших методов.
Что почитать
- Legendre P., Legendre L. (1998) Numerical ecology. Second english edition. Elsevier, Amsterdam. (Фундаментальный труд, описывающий большинство методов. Дается исчерпывающее обсуждение разнообразных коэффициентов сходства/различия)
- Zuur, A. F., Ieno, E. N., Smith, G. M. Analysing Ecological Data. Springer 2007 (Практически все то же самое, что в L&L, но написанное простым языком)
- Clarke, K. R., Gorley R. N. (2006) PRIMER v6: User Manual/Tutorial. PRIMER-E, Plymouth. (Очень доходчиво написанное руководство, дающее общее представление о “механике” работы многомерных методов)
- Миркин Б.М., Розенберг Г.С. Фитоценология. Принципы и методы. М., 1978. (Руководство написано в докомпьютерную эпоху, но простейшие методы изложены очень хорошо)
- Василевич В.И. Статистические методы в геоботанике. - Л.: Наука, 1969.
- Дюран Б., Оделл П. Кластерный анализ. М.: Статистика, 1977