class: middle, left, inverse, title-slide .title[ # Моделирование структуры дисперсии в смешанных моделях ] .subtitle[ ## Линейные модели… ] .author[ ### Марина Варфоломеева, Вадим Хайтов, Анастасия Лянгузова ] .date[ ### Осень 2024 ] --- ## Вы узнаете - как бороться с гетерогенностью дисперсии; - что такое обобщённый метод наименьших квадратов. ### Вы сможете - применять обобщённые линейные модели, включающие ковариату дисперсии; - подобрать функцию, которая свяжет величину дисперсии с ковариатой дисперсии так, чтобы правдоподобие (likelihood) было бы максимальным; - смоделировать структуру дисперсии для модели, включающей дискретные предикторы и случайные факторы. --- class: middle, center, inverse # Пример --- сексуальная активность мух --- ## Зависит ли продолжительность жизни самцов от их сексуальной активности? .pull-left[  .tiny[ from [Shutterstock](https://www.shutterstock.com/ru/image-photo/fruit-flies-drosophila-red-eyes-625417247) ] ] .pull-right[ Вопрос исследования: Зависит ли продолжительность жизни самца от его половой активности? __Зависимая переменная:__ - `longevity` --- Продолжительность жизни самца (количество дней); __Предикторы:__ - `activity` --- дискретный фактор, характеризующий условия активности самцов; - `thorax` --- длина груди, непрерывная величина (мм). ] --- ## Дизайн эксперимента .pull-left[  ] .pull-right[ В фокусе исследования переменная `activity` однако известно, что крупные самцы живут дольше мелких. В качестве ковариаты взят размер самца `thorax`. ] --- ## Читаем данные ``` r library(faraway) data(fruitfly) fly <- fruitfly # Переименуем датасет для краткости str(fly) ``` ``` 'data.frame': 124 obs. of 3 variables: $ thorax : num 0.68 0.68 0.72 0.72 0.76 0.76 0.76 0.76 0.76 0.8 ... $ longevity: int 37 49 46 63 39 46 56 63 65 56 ... $ activity : Factor w/ 5 levels "isolated","one",..: 4 4 4 4 4 4 4 4 4 4 ... ``` --- ## Проверяем данные ``` r # Есть ли пропущенные значения? colSums(is.na(fly)) ``` ``` thorax longevity activity 0 0 0 ``` ``` r # Сколько измерений по каждой из градаций? table(fly$activity) ``` ``` isolated one low many high 25 25 25 24 25 ``` --- ## Нет ли выбросов: пишем код ``` r library(ggplot2) theme_set(theme_bw()) gg_dot <- ggplot(fly, aes(y = 1:nrow(fly))) + geom_point() Pl1 <- gg_dot + aes(x = longevity) Pl2 <- gg_dot + aes(x = thorax) ``` --- ## Нет ли выбросов: строим диаграммы Кливленда ``` r library(cowplot) plot_grid(Pl1, Pl2) ``` <!-- --> Выбросов нет. --- ## Нет ли коллинеарности ``` r ggplot(fly, aes(x = activity, y = thorax)) + geom_boxplot() ``` <!-- --> Коллинеарности предикторов нет. --- ## Гипотеза и модель Гипотеза: Продолжительность жизни зависит от половой активности. Модель: `$$Longivity_{i} = \beta_0 + \beta_1 Thorax_{i} + \beta_{2} I_{isolated} + \beta_{3} I_{one} + \beta_{4} I_{many} + \beta_{5} I_{low} + \\ + Interactions + \varepsilon_{i}$$` `$$\varepsilon_{i} \sim N(0, \sigma^2)$$` --- ## Код для подгонки модели ``` r mod_formula <- longevity ~ thorax*activity M1 <- lm(mod_formula, data = fruitfly) library(car) Anova(M1) ``` ``` Anova Table (Type II tests) Response: longevity Sum Sq Df F value Pr(>F) thorax 12368 1 107.77 < 2e-16 *** activity 9635 4 20.99 5.5e-13 *** thorax:activity 24 4 0.05 0.99 Residuals 13083 114 --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ``` --- ## Диагностика модели ``` r M1_diagn <- fortify(M1) ggplot(M1_diagn, aes(x = .fitted, y = .stdresid)) + geom_point() + geom_hline(yintercept = 0) ``` <!-- --> Мы не можем доверять результатам оценки, так как присутствуют явные признаки гетероскедастичности. --- ## Чем опасна гетероскедастичность .pull-left-60[ Возьмем 1000 выборок из этих совокупностей по 10 наблюдений и построим много линейных моделей ``` r N <- 1000; b_0 <- 0; b_1 <- 0 # нет гетероскедастичности set.seed(123456) x <- rnorm(N, 10, 3) eps_1 <- rnorm(N, 0, 10) y_1 <- b_0 + b_1*x + eps_1 # есть гетероскедастичность h <- function(x) x^(2*0.7) eps_2 <- rnorm(N, 0, h(x)) y_2 <- b_0 + b_1*x + eps_2 dat2 <- data.frame(x, y_1, y_2) p_values <- data.frame(p_no_heter = rep(NA, 1000), p_heter = NA) for(i in 1:1000){ df <- dat2[sample(1:1000, 10), ] M_no_heter <- lm(y_1 ~ x, data = df) M_heter <- lm(y_2 ~ x, data = df) p_values$p_no_heter[i] <- summary(M_no_heter)$coefficients[2, 4] #p-value из summary модели p_values$p_heter[i] <- summary(M_heter)$coefficients[2, 4] #p-value из summary модели } ``` ] .pull-right-40[ - Нет гетероскедастичности и нет связи между `\(y\)` и `\(x\)` (справедлива `\(H_0\)`) частота ошибок составляет. ``` r mean(p_values$p_no_heter < 0.05) ``` ``` [1] 0.039 ``` - Для совокупности с гетероскедастичностью, при отсутствии связи между `\(y\)` и `\(x\)` (справедлива `\(H_0\)`) частота ошибок составляет. ``` r mean(p_values$p_heter < 0.05) ``` ``` [1] 0.073 ``` ] --- class: middle, center, inverse # "Эволюция" регрессии --- ## Простая регрессионная модель $$ \mathbf Y = \mathbf X\boldsymbol\beta + \varepsilon $$ Фиксированная часть модели: `\(\mathbf X\boldsymbol\beta\)`. Случайная часть модели: `\(\varepsilon\)`. В моделях, основанных на нормальном распределении `\(\varepsilon \sim N(0, \sigma^2)\)`. **Важно!** Остатки независимы и одинаково распределены со средним 0 и дисперсией `\(\sigma^2\)`, одинаковой для всех уровней `\(y_i\)`. То есть остатки --- это шум, в котором нет каких-то паттернов. --- ## Смешанные модели 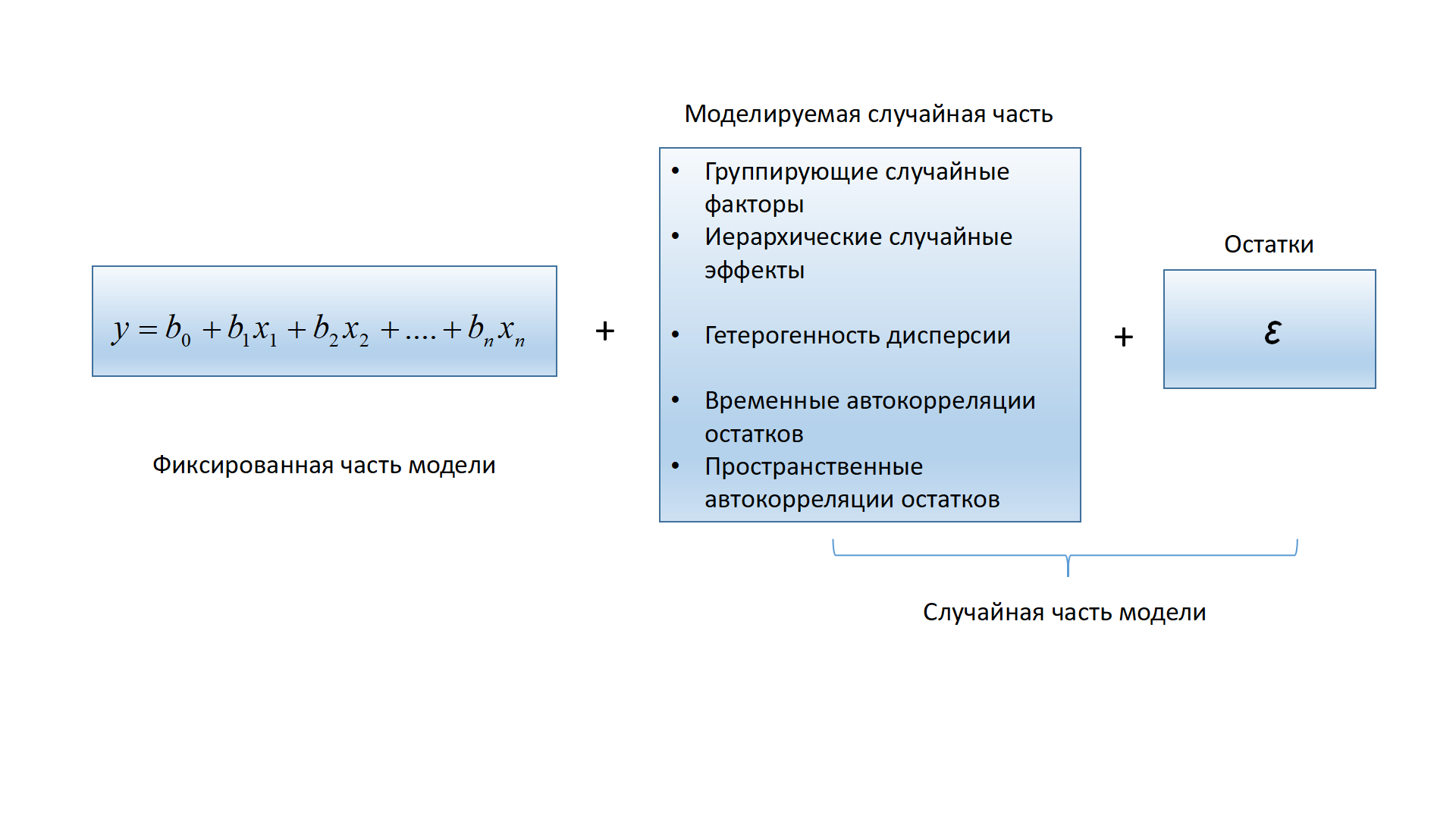 --- ## Смешанные модели на языке матриц Смешанная линейная модель с группирующими факторами: $$ \mathbf Y_i = \mathbf X_i\boldsymbol\beta + \mathbf Z_i\mathbf b_i + \varepsilon_i $$ $$ \varepsilon _i \sim N(0, \boldsymbol\Sigma_i) $$ $$ \mathbf b_i \sim N(0, \mathbf{D}) $$ --- ## Расширенная смешанная линейная модель $$ \mathbf Y_i = \mathbf X_i\boldsymbol\beta + \mathbf Z_i \mathbf b_i + \varepsilon_i $$ $$ \varepsilon _i \sim N(0, \sigma^2 \boldsymbol{\Lambda}_i) $$ Поведение остатков в пределах групп, связанных со случайными факторами, модифицируется (моделируется) матрицей `\(\Lambda\)`. $$ \mathbf b_i \sim N(0, \mathbf{D}) $$ --- ## Ковариата дисперсии (Variance covariate) Расширенная модель может включать еще один компонент: $$ \varepsilon \sim N(0, \sigma^2 \times \LARGE{f} \small(VC)) $$ `\(VC\)` --- ковариата дисперсии; `\(\LARGE{f} \small(VC)\)` --- функция, вводящая поправку, стабилизирующую дисперсию. В зависимости от формы функции `\(\LARGE{f} \small(VC)\)` мы получим разную структуру дисперсии в модели. --- class: middle, center, inverse # Generalized Least Squares --- ## Обобщенный метод наименьших квадратов (Generalized Least Squares) .pull-left[ ### Обычный метод наименьших квадратов (OLS): Ищем вектор `\(\textbf{b}\)` при котором `\(\Sigma \textbf e^2 = min\)`. Т.е. все остатки равнозначны. ] .pull-right[ ### Обобщённый метод наименьших квадратов (GLS): Ищем вектор `\(\textbf{b}\)`, при котором `\(\Sigma (\textbf e' \times\textbf W) = min\)`. Матрица `\(\textbf W\)` --- весовая матрица. Функция `gls` из пакета `nlme`. Если есть случайные факторы --- `lme`. ] .center[ Если `\(\textbf W = \textbf I\)`, то GLS = OLS. ] --- ## GLS модель и ее диагностика ``` r library(nlme) M1_gls <- gls(mod_formula, data = fruitfly) Pl_resid_M1_gls <- qplot(x = fitted(M1_gls), y = residuals(M1_gls, type = "pearson")) + geom_hline(yintercept = 0) Pl_resid_M1_gls ``` 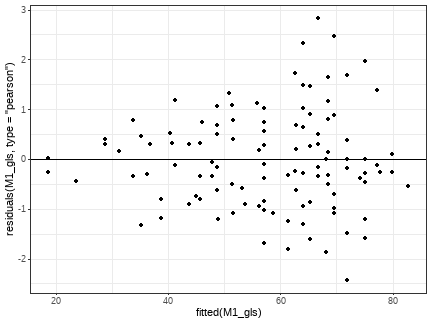<!-- --> --- ## Особенности функции `gls()` Если ничего не менять, функция `gls()` дает результаты полностью идентичные результатам функции `lm()`. Для оценки параметров по умолчанию используется Restricted Maximum Likelihood (REML). Этот метод дает более точные оценки случайных факторов, чем обычный ML. __Внимание!__ Модели, подобранные с помощью REML, можно сравнивать только если у них одинаковая фиксированная часть! --- ## Моделирование дисперсии Основная идея: Дисперсия закономерно изменяется в ответ на влияние некоторой ковариаты. Задача: подобрать функцию, которая свяжет величину дисперсии с ковариатой дисперсии так, чтобы правдоподобие (likelihood) было бы максимальным. Для подбора оптимальной структуры дисперсии мы будем работать со случайной частью модели, поэтому вместо ML оценки производятся с помощью REML. --- class: middle, center, inverse # Дисперсия зависит от непрерывной ковариаты --- ## Фиксированная структура дисперсии: varFixed() Дисперсия изменяется пропорционально значениям ковариаты дисперсии $$ \varepsilon_i \sim N(0, \sigma^2 \times VC_i) $$ Предположим, что дисперсия меняется пропорционально размеру груди мух (`thorax`). ``` r M2_gls <- gls(mod_formula, data = fly, weights = varFixed(~ thorax)) ``` Вопрос: Как выяснить, стала ли модель лучше? --- ## Можем сравнить две модели при помощи AIC ``` r AIC(M1_gls, M2_gls) ``` ``` df AIC M1_gls 11 892.3 M2_gls 11 889.7 ``` --- ## Что есть в summary от модели? ``` r summary(M2_gls) ``` ``` Generalized least squares fit by REML Model: mod_formula Data: fly * AIC BIC logLik * 889.7 919.8 -433.9 Variance function: Structure: fixed weights Formula: ~thorax *Coefficients: Value Std.Error t-value p-value (Intercept) -51.53 20.63 -2.498 0.0139 thorax 137.67 24.81 5.549 0.0000 activityone 10.26 31.82 0.322 0.7477 activitylow -9.10 32.21 -0.283 0.7780 activitymany -1.62 31.19 -0.052 0.9586 activityhigh -10.34 29.43 -0.351 0.7260 thorax:activityone -9.19 38.51 -0.239 0.8118 thorax:activitylow 2.49 38.66 0.064 0.9488 thorax:activitymany 7.19 38.10 0.189 0.8507 thorax:activityhigh -11.93 36.20 -0.330 0.7423 * Correlation: (Intr) thorax actvtyn actvtyl actvtym actvtyh thrx:ctvtyn thorax -0.995 activityone -0.648 0.645 activitylow -0.640 0.637 0.415 activitymany -0.661 0.658 0.429 0.424 activityhigh -0.701 0.697 0.455 0.449 0.464 thorax:activityone 0.641 -0.644 -0.996 -0.410 -0.424 -0.449 thorax:activitylow 0.638 -0.642 -0.414 -0.996 -0.422 -0.447 0.413 thorax:activitymany 0.648 -0.651 -0.420 -0.415 -0.995 -0.454 0.420 thorax:activityhigh 0.682 -0.685 -0.442 -0.437 -0.451 -0.995 0.442 thrx:ctvtyl thrx:ctvtym thorax activityone activitylow activitymany activityhigh thorax:activityone thorax:activitylow thorax:activitymany 0.418 thorax:activityhigh 0.440 0.446 Standardized residuals: Min Q1 Med Q3 Max -2.35171 -0.62456 -0.07116 0.60697 2.83272 Residual standard error: 11.69 Degrees of freedom: 124 total; 114 residual ``` --- ## Что есть в summary от модели? Помимо информационных критериев и коэффициентов модели `summary` содержит корреляционную матрицу. Из неё можно извлечь значения дисперсии для параметров модели (лежат на главной диагонали), а также коэффициенты корреляции между параметрами. Последние можно использовать для оценки мультиколлинеарности. ``` r cov2cor(vcov(M2_gls)) # получаем те же значения, что в выводе summary от модели ``` ``` (Intercept) thorax activityone activitylow activitymany (Intercept) 1.0000 -0.9947 -0.6484 -0.6404 -0.6615 thorax -0.9947 1.0000 0.6450 0.6370 0.6579 activityone -0.6484 0.6450 1.0000 0.4153 0.4289 activitylow -0.6404 0.6370 0.4153 1.0000 0.4236 activitymany -0.6615 0.6579 0.4289 0.4236 1.0000 activityhigh -0.7010 0.6973 0.4545 0.4490 0.4637 thorax:activityone 0.6408 -0.6443 -0.9955 -0.4104 -0.4239 thorax:activitylow 0.6384 -0.6418 -0.4139 -0.9956 -0.4222 thorax:activitymany 0.6478 -0.6512 -0.4200 -0.4149 -0.9952 thorax:activityhigh 0.6817 -0.6853 -0.4420 -0.4366 -0.4509 activityhigh thorax:activityone thorax:activitylow (Intercept) -0.7010 0.6408 0.6384 thorax 0.6973 -0.6443 -0.6418 activityone 0.4545 -0.9955 -0.4139 activitylow 0.4490 -0.4104 -0.9956 activitymany 0.4637 -0.4239 -0.4222 activityhigh 1.0000 -0.4492 -0.4475 thorax:activityone -0.4492 1.0000 0.4135 thorax:activitylow -0.4475 0.4135 1.0000 thorax:activitymany -0.4541 0.4196 0.4179 thorax:activityhigh -0.9946 0.4415 0.4398 thorax:activitymany thorax:activityhigh (Intercept) 0.6478 0.6817 thorax -0.6512 -0.6853 activityone -0.4200 -0.4420 activitylow -0.4149 -0.4366 activitymany -0.9952 -0.4509 activityhigh -0.4541 -0.9946 thorax:activityone 0.4196 0.4415 thorax:activitylow 0.4179 0.4398 thorax:activitymany 1.0000 0.4463 thorax:activityhigh 0.4463 1.0000 ``` --- ## Степенная зависимость дисперсии от ковариаты: varPower() $$ \varepsilon_{ij} \sim N(0, \sigma^2 \times |VC|^{2\delta}) $$ Параметр `\(\delta\)` неизвестен и требует оценки. Если `\(\delta = 0\)`, то структура дисперсии будет аналогична структуре дисперсии в "обычной" регрессионной модели, где `\(\varepsilon \sim N(0, \sigma^2)\)`. **Важно!** Если значения ковариаты дисперсии могут принимать значение равное нулю, то такая форма структуры дисперсии не определена и использоваться не может. ``` r M3_gls <- gls(mod_formula, data = fly, weights = varPower(form = ~ thorax)) ``` --- ## Что произошло в результате работы функции `varPower()`? ``` r summary(M3_gls) ``` Часть вывода `summary(M3_gls)`: ``` Variance function: Structure: Power of variance covariate Formula: ~thorax Parameter estimates: power 1.987254 ``` `$$\varepsilon_{ij} \sim N(0, \sigma^2 \times |VC|^{2\delta})$$` Оценка параметра `\(\delta\)` ``` r M3_gls$modelStruct ``` ``` varStruct parameters: power 1.987 ``` --- ## Степенная зависимость дисперсии от ковариаты для разных уровней дискретного фактора ``` r M4_gls <- gls(mod_formula, data = fly, weights = varPower(form = ~ thorax|activity)) ``` Подобранные параметры ``` r M4_gls$modelStruct ``` ``` varStruct parameters: many isolated one low high 1.862 1.681 0.786 1.419 3.334 ``` --- ## Экспоненциальная зависимость дисперсии от ковариаты: varExp() $$ \varepsilon_{ij} \sim N(0, \sigma^2 \times e^{2\delta \times VC_i}) $$ Эта форма структуры дисперсии может применяться для случаев, когда `\(VC = 0\)`. Если `\(\delta = 0\)`, то структура дисперсии будет аналогична структуре дисперсии в "обычной" регрессионной модели, то есть `\(\varepsilon_{ij} \sim N(0, \sigma^2)\)`. ``` r M5_gls <- gls(mod_formula, data = fly, weights = varExp(form = ~ thorax)) M6_gls <- gls(mod_formula, data = fly, weights = varExp(form = ~ thorax|activity)) ``` --- ## Подобранные параметры ``` r M5_gls$modelStruct ``` ``` varStruct parameters: expon 2.443 ``` ``` r M6_gls$modelStruct ``` ``` varStruct parameters: many isolated one low high 1.660 1.963 2.101 1.934 1.441 ``` --- ## Усложненная степенная зависимость дисперсии от ковариаты $$ \varepsilon_{ij} \sim N(0, \sigma^2 \times (\delta_1 + |VC|^{2\delta_2})^2) $$ То есть подбирается не только показатель степени `\(\delta_2\)`, но еще и константа `\(\delta_1\)`. При `\(\delta_1=0\)` и `\(\delta_2=0\)` выражение `\(\varepsilon_{ij} \sim N(0,\sigma^2 \times (0 + |VC|^{0})\)` будет эквивалентно `\(\varepsilon_{ij} \sim N(0, \sigma^2)\)`. ``` r M7_gls <- gls(mod_formula, data = fly, weights = varConstPower(form = ~ thorax)) M8_gls <- gls(mod_formula, data = fly, weights = varConstPower(form = ~ thorax|activity)) ``` --- ## Что произошло в результате работы функции `varConstPower()`? `$$\varepsilon_{ij} \sim N(0, \sigma^2 \times (\delta_1 + |VC|^{2\delta_2})^2)$$` ``` r M7_gls$modelStruct ``` ``` varStruct parameters: const power -15.867 1.987 ``` ``` r M8_gls$modelStruct ``` ``` varStruct parameters: const.many const.isolated const.one const.low const.high -17.24327 -0.03472 0.04990 0.16843 -0.96133 power.many power.isolated power.one power.low power.high -0.56206 3.89001 2.70688 8.26979 3.08716 ``` --- class: middle, center, inverse # Дисперсия зависит от дискретного фактора --- ## Разные дисперсии для разных уровней категориальных предикторов: varIdent() $$ \varepsilon_{ij} \sim N(0, \sigma^2_j) $$ При построении моделей с такой структурой дисперсии подбирается `\(k - 1\)` новых параметров, где `\(k\)` --- количество уровней категориального предиктора. ``` r M9_gls <- gls(mod_formula, data = fly, weights = varIdent(form = ~1|activity)) ``` --- ## Что произошло в результате работы функции `varIdent()`? ``` r summary(M9_gls) ``` Часть вывода `summary(M9_gls)`: ``` Variance function:` Structure: Different standard deviations per stratum Formula: ~1 | activity Parameter estimates: many isolated one low high 1.0000000 1.4269619 1.5332811 1.3764655 0.8608559 ``` `$$\varepsilon_{ij} \sim N(0, \sigma^2_j)$$` Т.е. в выводе `summary()` присутствуют оценки `\(\sigma^2_j\)` --- ## Комбинированная структура дисперсии: varComb() ``` r M10_gls <- gls(mod_formula, data = fly, weights = varComb(varIdent(form = ~ 1|activity), varFixed(~ thorax))) M11_gls <- gls(mod_formula, data = fly, weights = varComb(varIdent(form = ~ 1|activity), varPower(form = ~ thorax))) M12_gls <- gls(mod_formula, data = fly, weights = varComb(varIdent(form = ~1| activity), varExp(form = ~ thorax))) M13_gls <- gls(mod_formula, data = fly, weights = varComb(varIdent(form = ~ 1|activity), varConstPower(form = ~ thorax))) ``` --- class: middle, center, inverse # Моделирование гетерогенности дисперсий --- финальная модель --- ## Находим финальную модель ``` r AICs <- AIC(M1_gls, M2_gls, M3_gls, M4_gls, M5_gls, M6_gls, M7_gls, M8_gls, M9_gls, M10_gls, M12_gls,M13_gls) AICs ``` ``` df AIC M1_gls 11 892.3 M2_gls 11 889.7 M3_gls 12 888.3 M4_gls 16 889.3 M5_gls 12 888.6 M6_gls 16 888.9 M7_gls 13 890.3 M8_gls 21 896.5 M9_gls 15 889.8 M10_gls 15 888.2 M12_gls 16 889.0 M13_gls 17 890.7 ``` --- ## Финальная модель ``` r AICs[AICs$AIC == min(AICs$AIC), ] ``` ``` df AIC M10_gls 15 888.2 ``` ``` r summary(M10_gls)$call ``` ``` gls(model = mod_formula, data = fly, weights = varComb(varIdent(form = ~1 | activity), varFixed(~thorax))) ``` --- ## Диагностика финальной модели ``` r Pl_resid_M1_gls <- Pl_resid_M1_gls + ggtitle("Было") + labs(x = ".fitted", y = "Pearson resid.") Pl_resid_M10_gls <- qplot(x = fitted(M10_gls), y = residuals(M10_gls, type = "pearson")) + geom_hline(yintercept = 0) + ggtitle("Стало")+ labs(x = ".fitted", y = "Pearson resid.") library(cowplot) plot_grid(Pl_resid_M1_gls, Pl_resid_M10_gls) ``` 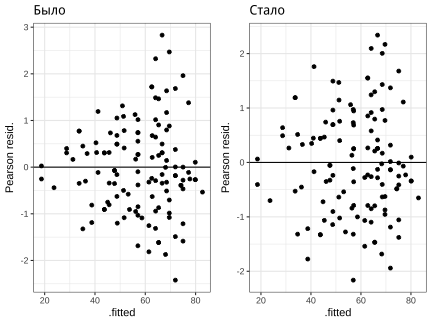<!-- --> --- class: middle, center, inverse ## Упрощение модели --- ### Задание: упростите модель -- Для упрощения финальной модели надо изменять фиксированную часть, REML не годится! ``` r M10_gls_ML <- update(M10_gls, method = "ML") drop1(M10_gls_ML, test = "Chi") ``` ``` Single term deletions Model: longevity ~ thorax * activity Df AIC LRT Pr(>Chi) <none> 946 thorax:activity 4 939 0.543 0.97 ``` --- ## Больше ничего упростить нельзя ``` r M10_gls_ML2 <- update(M10_gls_ML, .~.-thorax:activity) drop1(M10_gls_ML2, test = "Chi" ) ``` ``` Single term deletions Model: longevity ~ thorax + activity Df AIC LRT Pr(>Chi) <none> 939 thorax 1 1033 96.7 < 2e-16 *** activity 4 1001 70.4 1.9e-14 *** --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ``` --- ## Финальная модель и подготовка визуализации ``` r M10_final <- update(M10_gls_ML2, method = "REML") library(dplyr) new_data <- fly %>% group_by(activity) %>% do(data.frame(thorax = seq(min(.$thorax), max(.$thorax), length.out = 100))) X <- model.matrix(~ thorax + activity, data = new_data) b <- coef(M10_final) new_data$fitted <- X%*%b new_data$SE <- sqrt(diag(X %*% vcov(M10_final) %*% t(X))) ``` --- ## Визуализация финальной модели ``` r ggplot(new_data, aes(x = thorax, y = fitted, color = activity)) + geom_line() + geom_ribbon(aes(ymin = fitted - 2 * SE, ymax = fitted + 2 * SE, fill = activity), alpha = 0.5) + geom_point(data = fly, aes(x = thorax, y = longevity)) ``` 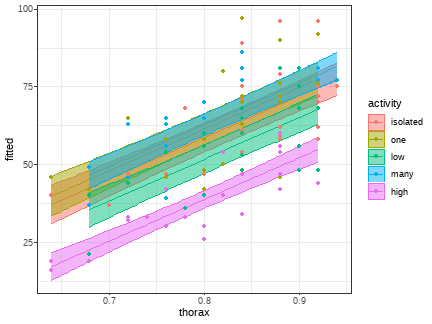<!-- --> --- class: middle, center, inverse # Моделирование структуры дисперсии при наличии случайных факторов --- ## Рост крыс при разной диете .pull-left[ ``` r data("BodyWeight") bw <- as.data.frame(BodyWeight) head(bw, 14) ``` ``` weight Time Rat Diet 1 240 1 1 1 2 250 8 1 1 3 255 15 1 1 4 260 22 1 1 5 262 29 1 1 6 258 36 1 1 7 266 43 1 1 8 266 44 1 1 9 265 50 1 1 10 272 57 1 1 11 278 64 1 1 12 225 1 2 1 13 230 8 2 1 14 230 15 2 1 ``` ] .pull-right[ Три группы крыс, содержались при разных условиях кормления 64 дня. Каждую крысу взвешивали с определенной периодичностью. Всего было изучено 16 особей. Задача: Построить модель, которая дала бы ответ на вопрос, изменяется ли характер роста крыс в зависимости от типа диеты? .tiny[ пример из книги Pinheiro and Bates, 2000 ] .tiny[ оригинальное исследование Hand and Crowder, 1996 ] ] --- ## Решение: Неправильная модель ``` r M1 <- gls(weight ~ Time*Diet, data = bw) ``` Вопрос: Почему такая модель неправильная? -- **Важно!** Строить простую линейную модель в данном случае *некорректно*! - Дизайн эксперимента изначально включает случайный фактор `Rat`. Здесь мы имеем дело с повторными наблюдениями одного и того же объекта. - Однако мы рассмотрим `M1` для демонстрации того, что происходит, если не учитывать этой особенности экспериментального дизайна. ``` r Anova(M1) ``` ``` Analysis of Deviance Table (Type II tests) Response: weight Df Chisq Pr(>Chisq) Time 1 19.55 0.0000098 *** Diet 2 2228.76 < 2e-16 *** Time:Diet 2 3.59 0.17 --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ``` --- ## Решение: Модель со случайными факторами Задание: напишите код для модели, включающей случайные факторы. -- ``` r M2 <- lme(weight ~ Time*Diet, data = bw, random = ~1|Rat) M3 <- lme(weight ~ Time*Diet, data = bw, random = ~1 + Time|Rat) ``` -- Какую из моделей выбрать? -- ``` r AIC(M2, M3) ``` ``` df AIC M2 8 1248 M3 10 1172 ``` --- ## Решение: Пытаемся ответить на вопрос исследования ``` r Anova(M3) ``` ``` Analysis of Deviance Table (Type II tests) Response: weight Chisq Df Pr(>Chisq) Time 82.6 1 < 2e-16 *** Diet 170.7 2 < 2e-16 *** Time:Diet 15.2 2 0.00051 *** --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ``` Наличие взаимодействия говорит о том, что экспериментальное воздействие повлияло на характер роста крыс. Но! можем ли мы доверять этим результатам? --- ## Диагностика модели ``` r diagnostic <- data.frame(.fitted = fitted(M3), .residuals = residuals(M3, type = "pearson"), Diet = bw$Diet, Time = bw$Time) Pl1 <- ggplot(diagnostic, aes(x=.fitted, y=.residuals) ) + geom_point() Pl2 <- ggplot(diagnostic, aes(x=Time, y=.residuals) ) + geom_point() Pl3 <- ggplot(diagnostic, aes(x=Diet, y=.residuals) ) + geom_boxplot() grid.arrange(Pl1, Pl2, Pl3, ncol=3) ``` <!-- --> Есть некоторые признаки гетерогенности дисперсии. --- ## Моделируем структуру дисперсии ``` r M3_1 <- update(M3, weights = varIdent(form = ~ 1|Diet)) M3_2 <- update(M3, weights = varPower(form = ~Time)) M3_3 <- update(M3, weights = varPower(form = ~Time|Diet)) M3_4 <- update(M3, weights = varConstPower(form = ~Time), control = list(msMaxIter = 1000, msMaxEval = 1000)) M3_5 <- update(M3, weights = varExp(form = ~Time)) M3_6 <- update(M3, weights = varExp(form = ~Time|Diet)) M3_7 <- update(M3, weights = varComb(varExp(form = ~Time), varIdent(form = ~1|Diet))) M3_8 <- update(M3, weights = varComb(varPower(form = ~Time), varIdent(form = ~1|Diet))) ``` --- ## Выбираем лучшую модель ``` r AIC(M3, M3_1, M3_2, M3_3, M3_5, M3_6, M3_7, M3_8) ``` ``` df AIC M3 10 1172 M3_1 12 1164 M3_2 11 1173 M3_3 13 1158 M3_5 11 1174 M3_6 13 1155 M3_7 13 1165 M3_8 13 1162 ``` --- ## Диагностика модели ``` r M3_6_diagn <- data.frame(.fitted = fitted(M3_6), .residuals = residuals(M3_6, type = "pearson"), Diet = bw$Diet, Time = bw$Time) Pl4 <- ggplot(M3_6_diagn, aes(x=.fitted, y=.residuals) ) + geom_point() Pl5 <- ggplot(M3_6_diagn, aes(x=Time, y=.residuals) ) + geom_point() Pl6 <- ggplot(M3_6_diagn, aes(x=Diet, y=.residuals) ) + geom_boxplot() grid.arrange(Pl1, Pl4, nrow = 1) ``` <!-- --> --- ## Диагностика модели ``` r grid.arrange(Pl5, Pl6, nrow = 1) ``` <!-- --> --- ## Отвечаем на вопрос ``` r Anova(M3_6) ``` ``` Analysis of Deviance Table (Type II tests) Response: weight Chisq Df Pr(>Chisq) Time 83.2 1 < 2e-16 *** Diet 169.3 2 < 2e-16 *** Time:Diet 17.3 2 0.00018 *** --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ``` Взаимодействие факторов осталось! --- ## Смотрим на предсказания модели ``` r MyData <- expand.grid(Time = unique(bw$Time), Diet = factor(1:3)) MyData$Predicted <- predict(M3_6, newdata = MyData, level = 0) ggplot(MyData, aes(x = Time, y = Predicted, color = Diet)) + geom_line(linewidth = 1.5) + geom_point(data = bw, aes(x = Time, y = weight), position = position_jitter()) ``` <!-- --> Углы наклона в разных группах различаются! --- ## Take-home messages При наличии признаков гетероскедастичности можно пойти тремя путями: 1. Произвести преобразование зависимой переменной; 2. Включить в модель элемент, описывающий связь дисперсии с ковариатой дисперсии; 3. Если природа данных позволяет, то построить модель, основанную на распределении Пуассона или отрицательном биномиальном распределении. --- ## Что почитать + Zuur, A.F. et al. 2009. Mixed effects models and extensions in ecology with R. - Statistics for biology and health. Springer, New York, NY. + Pinheiro J, Bates D (2000) Mixed effects models in S and S-Plus. Springer-Verlag, New York, USA