Описание, проверка значимости и валидности линейных моделей

.title[
# Описание, проверка значимости и валидности линейных моделей
]
.subtitle[
## Линейные модели…
]
.author[
### Марина Варфоломеева, Вадим Хайтов, Анастасия Лянгузова
]
.date[
### Осень 2024
]

---

# Описание и проверка значимости линейных моделей

## Вы сможете

- Подобрать линейную модель зависимости переменной-отклика от одного предиктора
- Протестировать значимость линейной модели в целом и значимость отдельных ее коэффициентов при помощи t и F критериев
- Проверить условия применимости линейной регрессии при помощи графиков

---

# Вспомним пример из прошлой лекции

---

## Пример: IQ и размеры мозга

Зависит ли уровень интеллекта от размера головного мозга? (Willerman et al. 1991)

![Scan_03_11](images/MRI-Scan_03_11-by_bucaorg_Paul_Burnett_no_Flickr.jpg)

[Scan_03_11](https://flic.kr/p/c45eZ3) by bucaorg(Paul_Burnett) on Flickr

]

Было исследовано 20 девушек и 20 молодых людей

У каждого индивида измеряли:

- вес
- рост
- размер головного мозга (количество пикселей на изображении ЯМР сканера)
- Уровень интеллекта измеряли с помощью IQ тестов

Пример: Willerman, L., Schultz, R., Rutledge, J. N., and Bigler, E. (1991), "In Vivo Brain Size and Intelligence", Intelligence, 15, p.223--228. 
Данные: ["The Data and Story Library"](http://lib.stat.cmu.edu/DASL) 
Фото: [Scan\_03\_11](https://flic.kr/p/c45eZ3) by bucaorg (Paul Burnett) on Flickr

]

---

## Вспомним, на чем мы остановились

```

Call:
lm(formula = PIQ ~ MRINACount, data = brain)

Residuals:
   Min     1Q Median     3Q    Max 
 -39.6  -17.9   -1.6   17.0   42.3

Coefficients:
              Estimate Std. Error t value Pr(>|t|)  
(Intercept)  1.7437570 42.3923825    0.04    0.967  
MRINACount   0.0001203  0.0000465    2.59    0.014 *
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 21 on 38 degrees of freedom
Multiple R-squared:  0.15,	Adjusted R-squared:  0.127 
F-statistic: 6.69 on 1 and 38 DF,  p-value: 0.0137
```

---

## Уравнение и график зависимости

`$$PIQ_i = 1.744 + 0.0001202 \cdot MRINACount_i$$`

![](07_model_description_and_validation_files/figure-html/unnamed-chunk-3-1.png)

---

# Тестирование гипотез о линейных моделях
 
---
 
## Способы проверки значимости модели и ее коэффициентов

Два равноправных способа

### Значима ли модель целиком?

+ F критерий

### Значима ли связь между предиктором и откликом?

+ t-критерий

+ F-критерий

---

# Тестирование гипотез с помощью t-критерия

---

## Тестирование гипотез с помощью t-критерия

### Гипотезы

Зависимость есть, если `$\beta_k \ne 0$`

Нулевая гипотеза `$H_0: \beta_k = 0$`

---

## Тестирование гипотез с помощью t-критерия

### Гипотезы

Зависимость есть, если `$\beta_k \ne 0$`

Нулевая гипотеза `$H_0: \beta_k = 0$`

### Тестовая статистика

`$$t=\frac{b_k - \beta_k}{SE_{b_k}} = \frac{b_k - 0}{SE_{b_k}} = \frac{b_k}{SE_{b_k}}$$`

Число степеней свободы: `$df = n − p$`, где `$n$` — объем выборки, `$p$` — число параметров модели, `$k$` — конкретный коэффициент регрессии.

Для простой линейной регрессии с одним предиктором `$df = n - 2$`.

---

## Зависит ли IQ от размера головного мозга?

`$$PIQ_i = 1.744 + 0.0001202 \cdot MRINACount_i$$`

``` r
summary(brain_model)
```

```

Call:
lm(formula = PIQ ~ MRINACount, data = brain)

Residuals:
   Min     1Q Median     3Q    Max 
 -39.6  -17.9   -1.6   17.0   42.3

Residual standard error: 21 on 38 degrees of freedom
Multiple R-squared:  0.15,	Adjusted R-squared:  0.127 
F-statistic: 6.69 on 1 and 38 DF,  p-value: 0.0137
```

Результаты теста на IQ статистически значимо связаны с размерами мозга на МРТ ( `$t_{ 0.05, 38}$` = 2.59, `$p$` = 0.01 ).

---

# Тестирование гипотез при помощи F-критерия

---

## Общая изменчивость

Общая изменчивость `$SS_{t}$` — это сумма квадратов отклонений наблюдаемых значений `$y_i$` от общего среднего `$\bar y$`

![](07_model_description_and_validation_files/figure-html/unnamed-chunk-7-1.png)

---

## Структура общей изменчивости

`$$SS_t = \color{blue}{SS_r} + \color{green}{SS_e}$$`

![](07_model_description_and_validation_files/figure-html/unnamed-chunk-8-1.png)

---

## От изменчивостей к дисперсиям

![](07_model_description_and_validation_files/figure-html/unnamed-chunk-9-1.png)

| `$MS_t$`, полная дисперсия | `$\color{blue}{MS_r}$`, дисперсия, объясненная регрессией | `$\color{green}{MS_e}$`, остаточная дисперсия | 
|-----|-----|-----|
| `$MS_{t} =\frac{SS_{t}}{df_{t}}$` | `$\color{blue}{MS_{r}} =\frac{\color{blue}{SS_{r}}}{df_{r}}$` | `$\color{green}{MS_{e}} =\frac{\color{green}{SS_{e}}}{df_{e}}$` |
| `$SS_{t}=\sum{(y_i - \bar{y})^2}$` | `$\color{blue}{SS_{r}}=\sum{(\hat{y}-\bar{y})^2}$` | `$\color{green}{SS_{e}}=\sum{(y_i - \hat{y})^2}$` |
| `$df_{t} = n-1$` | `$df_{r} = 1$` | `$df_{e} = n-2$` |

---

## С помощью `$MS_r$` и `$MS_e$` можно тестировать значимость коэффициентов

Если дисперсии остатков для всех значений x равны, то

`$E(\color{blue}{MS_r}) = \color{green}{\sigma^2} + \color{red}{\beta_1}^2\sum(x_i - \bar x)^2$` 
--
`$= \color{green}{\sigma^2} + \sigma_{x}^2$`

`$E(\color{green}{MS_e}) = \color{green}{\sigma^2}$`

Если зависимости нет, то `$\color{red}{\beta_1} = 0$`, и тогда

`$\color{blue}{MS_r} \approx \color{green}{MS_e}$`

Мы хотим протестировать гипотезы:

- `$H_0: \color{red}{\beta_1} = 0$`
- `$H_A: \color{red}{\beta_1} \ne 0$`

Если справедлива `$H_A: \color{red}{\beta_1} \ne 0$`, то `$\color{blue}{MS_r} > \color{green}{MS_e}$`

`$$F= \frac{\color{blue}{MS _{r}}}{\color{green}{MS_{e}}}$$`
--

Поздравляю, вы только что изобрели _F_-критерий!

---

## Тестирование значимости коэффициентов регрессии при помощи F-критерия

`$$F_{df_r, df_e}= \frac{\color{blue}{MS _{r}}}{\color{green}{MS_{e}}}$$`

Для простой линейной регрессии  
`$df_{r} = 1$` и `$df_{e} = n - 2$`

![](07_model_description_and_validation_files/figure-html/f-distr-1.png)

]

- У F-распределения два параметра: `$df_{r}$` и `$df_{e}$`

- Логика F-теста аналогична t-критерию: Определяем вероятность того, что при *условии справедливости `$H_0$`* при повторных выборках появится значение F больше или равное F, полученному в нашем эксперименте.

- F-тест будет односторонним, т.к. соотношение дисперсий может быть только положительным.

]

---

## Таблица результатов дисперсионного анализа

| Источник изменчивости  | df | SS | MS | F  | 
| ----- | ----- | ----- | ----- | ----- | 
| .blue[Регрессия] | `$df _r = 1$` | `$\color{blue}{SS _r} = \sum{(\hat y _i - \bar y)^2}$` | `$\color{blue}{MS _r} = \frac{\color{blue}{SS _r}}{df _r}$` | `$F _{df _r, df _e} = \frac{\color{blue}{MS _r}}{\color{green}{MS _e}}$` | 
| .green[Остаточная]|  `$df _e = n - 2$` | `$\color{green}{SS _e} = \sum{(y _i - \hat y _i)^2}$` | `$\color{green}{MS _e} = \frac{\color{green}{SS _e}}{df _e}$` | 
| Общая | `$df _t = n - 1$` | `$SS _t = \sum {(y _i - \bar y)^2}$` |

Минимальное упоминание результатов в тексте должно содержать `$F _{df _r, df _e}$` и `$p$`.

---

# Оценка качества подгонки модели

---

## В чем различие между этими двумя моделями?

![](07_model_description_and_validation_files/figure-html/residuals-scatter-1.png)

У этих моделей разный разброс остатков:

- Модель слева объясняет практически всю изменчивость
- Модель справа объясняет не очень много изменчивости

---

## Коэффициент детерминации — мера качества подгонки модели

__Коэффициент детерминации__ описывает какую долю дисперсии зависимой переменной объясняет модель

`$$R^2 = \frac{\color{blue}{SS_{r}}}{SS_{t}}$$`

- `$0 < R^2 < 1$`
- `$R^2 = r^2$` — для простой линейной регрессии коэффициент детерминации равен квадрату коэффициента Пирсоновской корреляции

---

## Если в модели много предикторов, нужно внести поправку

__Скорректированный коэффициет детерминации__ (adjusted R-squared)

Применяется если необходимо сравнить две модели с разным количеством параметров

$$ R^2_{adj} = 1- (1-R^2)\frac{n-1}{n-p}$$

`$p$` - количество параметров в модели

Вводится штраф за каждый новый параметр

---

## Еще раз смотрим на результаты регрессионного анализа зависимости IQ от размеров мозга

``` r
summary(brain_model)
```

```

Call:
lm(formula = PIQ ~ MRINACount, data = brain)

Residuals:
   Min     1Q Median     3Q    Max 
 -39.6  -17.9   -1.6   17.0   42.3

Residual standard error: 21 on 38 degrees of freedom
Multiple R-squared:  0.15,	Adjusted R-squared:  0.127 
F-statistic: 6.69 on 1 and 38 DF,  p-value: 0.0137
```

Модель зависимости IQ от размеров мозга на МРТ объясняет всего лишь 15 % общей изменчивости IQ в этих данных.

Ценность такой модели сомнительна.

---

## Как записываются результаты регрессионного анализа в тексте статьи?

Мы показали, что связь между результатами теста на IQ и размером головного мозга на МРТ описывается моделью вида
 
IQ = 1.74 + 0.00012 MRINACount ( `$F_{1,38}$` = 6.686, p = 0.014, `$R^2$` = 0.15)

Пишем статью?

---

## Задание 1 & 2

Выполните задания 1 и 2 в одном из этих файлов:

- 07_task_assumptions_catsM.R
- 07_task_assumptions_GAG.R

---

# Зачем нужна диагностика линейных моделей

---
## Если стохастическая модель адекватна, то что мы можем сказать про остатки?

![](07_model_description_and_validation_files/figure-html/unnamed-chunk-11-1.png)

- Остатки --- это просто шум. Обычно считается, что `$\varepsilon_i \in N(0, \sigma)$`.

- В остатках не должно быть никаких закономерностей (паттернов).

---
## Зачем нужна диагностика модели? Разве тестов было недостаточно?

Пусть у нас есть некоторая модель, которая показывает зависимость `$V_1 = f(V_2, V_3, V_4, V_5)$`

``` r
dat <- read.table('data/orly_owl_Lin_4p_5_flat.txt')
fit <- lm(V1 ~ V2 + V3 + V4 + V5, data = dat)
summary(fit)
```

```

Call:
lm(formula = V1 ~ V2 + V3 + V4 + V5, data = dat)

Residuals:
   Min     1Q Median     3Q    Max 
-2.065 -0.988  0.142  0.796  1.956

Coefficients:
 Estimate Std. Error t value Pr(>|t|) 
(Intercept) 0.00119 0.02117 0.06 0.96 
V2 0.98633 0.12863 7.67 2.6e-14 ***
V3 0.97229 0.12751 7.63 3.5e-14 ***
V4 0.86143 0.12043 7.15 1.1e-12 ***
V5 0.92747 0.08443 10.98 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1 on 2293 degrees of freedom
Multiple R-squared: 0.05,	Adjusted R-squared: 0.0483 
F-statistic: 30.2 on 4 and 2293 DF, p-value: <2e-16
```

Все значимо!

Пишем статью?

---

## Остатки модели

Постройте график зависимости остатков от предсказанных значений при помощи этого кода

``` r
library(car)
residualPlot(fit, pch = ".")
```

---

## Oh, really?

``` r
library(car)
residualPlot(fit, pch = ".")
```

![](07_model_description_and_validation_files/figure-html/bird-1.png)

[http://www4.stat.ncsu.edu/~stefanski/NSF_Supported/Hidden_Images/stat_res_plots.html](http://www4.stat.ncsu.edu/~stefanski/NSF_Supported/Hidden_Images/stat_res_plots.html)

В остатках скрыта информация!

---

## Анализ остатков линейных моделей

Этот анализ дает возможность:

1) Проверить данные на наличие влиятельных наблюдений и выявить их;

2) Проверить соответствует ли построенная модель условиям применимости линейных моделей.

---

## Условия применимости линейных моделей

1. Линейная связь
1. Независимость наблюдений
1. Соответствие нормальному распределению
1. Гомогенность дисперсий
1. Отсутствие коллинеарности предикторов (для множественной регрессии)

---

# Анализ остатков

---

## Какие бывают остатки?

### "Сырые" остатки
`$$\color{green}{e_i} = y_i - \color{blue}{\hat{y_i}}$$`

### Стандартизованные (стьюдентизированные) остатки

`$$s_i = \frac{\color{green}{e_i}}{\sqrt{MS_e(1-\color{purple}{h_{ii}})}}$$`

- легко сравнивать (стандартизованы), учитывают силу влияния наблюдений

<hr />

- `$\sqrt{MS_e}$` — стандартное отклонение остатков
- `$\color{purple}{h_{ii}}$` — "сила воздействия" отдельных наблюдений (leverage, рычаг проекционной матрицы)

---

## Что такое проекционная матрица?

По определению, остатки `$\color{green}{\mathbf{e}} = \mathbf{Y} - \color{blue}{\hat{\mathbf{Y}}}$`.

Тогда `$\color{green}{\mathbf{e}} = \mathbf{Y} - \mathbf{X} \mathbf{b} = \mathbf{Y} - \mathbf{X}[\mathbf{X}'\mathbf{X}]^{-1}\mathbf{X}'\mathbf{Y}$`.

Обозначим  `$\color{purple}{\mathbf{H}} \equiv  \mathbf{X}[\mathbf{X}'\mathbf{X}]^{-1}\mathbf{X}'$`.

Матрица `$\color{purple}{\mathbf{H}}$` — называется __"хэт"-матрица__ (_hat-matrix_) или __проекционная матрица__, т.к. она позволяет получить предсказанные значения из наблюдаемых.

`$\color{blue}{\hat{\mathbf{Y}}} = \color{purple}{\mathbf{H}}\mathbf{Y}$`

Тогда остатки можно получить как `$\color{green}{\mathbf{e}} = \mathbf{Y} - \color{purple}{\mathbf{H}}\mathbf{Y} = (\mathbf{I} - \color{purple}{\mathbf{H}})\mathbf{Y}$`.

Диагональные элементы проекционной матрицы `$\color{purple}{h_{ii}}$` — это мера __воздействия__ точек на ход линии регрессии.

---

# Влиятельные наблюдения

---

## Влиятельные наблюдения (influential points)

Влиятельные наблюдения — это наблюдения, которые вносят слишком большой вклад в оценку параметров (коэффициентов) модели.

![](images/leverage.png)

Из кн. Quinn, Keough, 2002

Учет каких из этих точек повлияет на ход регрессии и почему?

- Точка 1 почти не повлияет, т.к. у нее маленький остаток, хоть и экстремальное значение `$X$`
- Точка 2 почти не повлияет, т.к. ее `$X$` близок к среднему, хоть и большой остаток
- Точка 3 повлияет сильно, т.к. у нее не только большой остаток, но и экстремальное значение `$X$`

---

## Воздействие точек (leverage)

__Воздействие__ точек `$\color{purple}{h_{ii}}$` (_leverage_) показывает силу влияния значений `$x_i$` на ход линии регрессии, то есть на `$\color{blue}{\hat{y_i}}$`

![](images/leverage.png)

Из кн. Quinn, Keough, 2002

]

![:scale 80%](images/seasaw-Weighing-Machine-by-neys-fadzil-on-Flickr.jpg)

Weighing Machine by neys fadzil on Flickr

]

Точки, располагающиеся дальше от `$\bar{x}$`, оказывают более сильное влияние на `$\color{blue}{\hat{y_i}}$`

- `$\color{purple}{h_{ii}}$` варьирует в промежутке от `$1/n$` до 1  
- Если  `$\color{purple}{h_{ii}} > 2(p/n)$`, то надо внимательно посмотреть на данное значение ( `$p$` — число параметров модели, `$n$` — объем выборки)

---

## Расстояние Кука (Cook's distance)

описывает, как повлияет на модель удаление данного наблюдения

`$$D_i = \frac{\sum{( \color{blue}{\hat{y_{j}}} - \color{red}{\hat{y}_{j(i)}})^2}}{p \; MS_e}$$`

- `$\color{blue}{\hat{y_j}}$` — значение предсказанное полной моделью
- `$\color{red}{\hat{y}_{j(i)}}$` — значение, предсказанное моделью, построенной без учета `$i$`-го значения предиктора
- `$p$` — количество параметров в модели
- `$MS_{e}$` — среднеквадратичная ошибка модели ( `$\hat\sigma^2$` )

---

## Расстояние Кука покажет оба аспекта влиятельности

Формулу расстояния Кука для данного `$i$`-того наблюдения можно расписать:

`$$D_i = \frac{\color{green}{e_i}^2}{p \; MS_e} \cdot \frac { \color{purple}{h_{ii}} } {(1 - \color{purple}{h_{ii}}) ^ 2}$$`

Видно, что `$D_i$` зависит сразу от

- `$\color{green}{e_i}$` — это величина остатков
- `$\color{purple}{h_{ii}}$` — это воздействие наблюдений

При каком значении `$D_i$` будем считать наблюдение выбросом?

Два варианта:

- `$D_i > 1$` — "мягкий" порог (для простоты в этом курсе такой)
- `$D_i > \frac{4}{(n - p)}$` —  "жесткий" порог ( `$n$` — объем выборки, `$p$` — число параметров)

---

## Что делать с наблюдениями-выбросами?

- Удалить?

__Осторожно!__ Только очевидные ошибки в наблюдениях можно удалять. Лучше найти причины.

- Трансформировать? Это не всегда поможет.
- Иногда можно переформулировать модель.

---

## Некоторые виды трансформаций

Трансформация  |  Формула  
------------- | -------------   
степень -2 | `$1/x^2$`
степень -1 | `$1/x$`
степень -0.5  | `$1/\sqrt{x}$`
степень 0.5 | `$\sqrt{x}$`
логарифмирование | `$log(x)$`

---

## Данные для анализа остатков

``` r
library(ggplot2)
brain_diag <- fortify(brain_model)
head(brain_diag, 2)
```

```
  PIQ MRINACount    .hat .sigma   .cooksd .fitted .resid .stdresid
1 124     816932 0.06638  20.88 0.0498380   99.98 24.017    1.1840
2 124    1001121 0.06687  21.27 0.0003039  122.13  1.868    0.0921
```

- `.hat` — "сила воздействия" данного наблюдения (leverage)
- `.cooksd` — расстояние Кука
- `.fitted` — предсказанные значения
- `.resid` — остатки
- `.stdresid` — стандартизованные остатки

---

## График расстояния Кука

Проверяем наличие влиятельных наблюдений в `brain_model`.

Порядок значений на графике такой же как в исходных данных.

``` r
# График расстояния Кука
ggplot(brain_diag, aes(x = 1:nrow(brain_diag), y = .cooksd)) + 
  geom_bar(stat = "identity")
```

![](07_model_description_and_validation_files/figure-html/gg-cook-1.png)

- Есть одно влиятельное наблюдение, которое нужно проверить, но сила его влияния невелика (расстояние Кука `$< 1$`, и только одно наблюдение больше `$4/(n-p) = 0.11$`)

---

## График остатков от предсказанных значений

Большую часть того, что нужно знать про остатки вы увидите на этом графике. А сейчас давайте научимся читать такой график.

``` r
gg_resid <- ggplot(data = brain_diag, aes(x = .fitted, y = .stdresid)) + 
 geom_point() + 
 geom_hline(yintercept = 0)
gg_resid
```

![](07_model_description_and_validation_files/figure-html/gg-resid-1.png)

---

# 1. Линейность связи

---

## Нелинейность связи видно на графиках остатков

![](07_model_description_and_validation_files/figure-html/non-linear-1.png)

__Проверка на линейность связи__

- График зависимости `$y$` от `$x$` (и от других переменных, не включенных в модель)
- График остатков от предсказанных значений

---

## Что делать, если связь нелинейна?

- Добавить неучтенные переменные или взаимодействия;
- Применить линеаризующее преобразование (Осторожно!);
- Применить обобщенную линейную модель с другой функцией связи (GLM);
- Построить аддитивную модель (GAM), если достаточно наблюдений по `$x$`;
- Построить нелинейную модель, если известна форма зависимости.

---

## Примеры линеаризующих преобразований

__Логарифмирование__

![](07_model_description_and_validation_files/figure-html/log-transform-1.png)

__Возведение в степень__, и т.д.

![](07_model_description_and_validation_files/figure-html/power-transform-1.png)

---

## Не стоит трансформировать отклик!

![](07_model_description_and_validation_files/figure-html/dep-var-transform-1.png)

__Осторожно!__ Вы рискуете изучить не то, что хотели:

1.При логарифмировании отклика вы будете изучать поведение мат.ожидания логарифма  
`$E(log(y_i)) = b_0 + b_1x_{1i} + ... + e_i$`.

2.Трансформация отклика не только линеаризует зависимость, но и затронет величину остатков `$e$`.

Вместо трансформации отклика лучше использовать обобщенную линейную модель с подходящей функцией связи, например:

`$log(E(y_i)) =  b_0 + b_1x_{1i}+ ... + e_i$`

---

# 2. Независимость

---

## Каждое значение `$y_i$` должно быть независимо от любого другого `$y_j$`

Это нужно контролировать на этапе планирования сбора материала

* Наиболее частые источники зависимостей: 
    + псевдоповторности (повторно измеренные объекты)
    + неучтенные переменные
    + временные автокорреляции (если данные - временной ряд)
    + пространственные автокорреляции (если пробы взяты в разных местах)
    + и т.п.

---

## Диагностика нарушений независимости

Взаимозависимости можно заметить на графиках остатков

- остатки vs. предсказанные значения
- остатки vs. переменные в модели
- остатки vs. переменные не в модели

---

## Нарушение независимости: Неучтенная переменная

![](07_model_description_and_validation_files/figure-html/unaccounted-var-1.png)

- Слева: Если в модели не учтена переменная `$X2$`, внешне все нормально, но величина остатков зависит от `$X2$`
- Справа: Если `$X2$` учесть, то зависимость остатков от `$X2$` исчезает

---

## Нарушение независимости: Автокорреляция

В данном случае, наблюдения — это временной ряд или ряд наблюдений в пространстве.

![](07_model_description_and_validation_files/figure-html/autocorr-1.png)

На графиках остатков четко видно, что остатки не являются независимыми. Наблюдения, расположенные на определенном расстоянии друг от друга, имеют остатки похожей величины.

---

## Чем опасна автокорреляция (и любая другая зависимость наблюдений друг от друга)

``` r
set.seed(123)
population <- rnorm(1000)
population_correlated <- arima.sim(list(order = c(1,0,0), ar = 0.5), n = 1000, sd=1)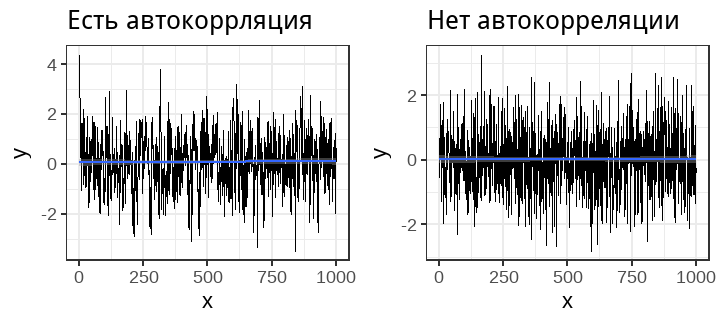
```

![](07_model_description_and_validation_files/figure-html/unnamed-chunk-18-1.png)

---

## Чем опасна автокорреляция (и любая другая зависимость наблюдений друг от друга)

Построим 1000 моделей на случайных выборках по 10 последовательных наблюдений

``` r
p_values <- data.frame(p_no_cor = rep(NA, 1000), p_cor = NA)

for(i in 1:1000){
 begin = sample(1:900, 1)
 x = begin:(begin + 9)
 y_cor = population_correlated[begin:(begin + 9)] #Случайная выборка из генеральной совокупности с автокорреляцией
 y = population[begin:(begin + 9)] #Случайная выборка из генеральной совокупности без автокорреляции
 df = data.frame(x, y_cor, y)
 M_no_cor <- lm(y ~ x, data = df)
 M_cor <- lm(y_cor ~ x, data = df)
 p_values$p_no_cor[i] <- summary(M_no_cor)$coefficients[2, 4] #p-value из summary модели 
 p_values$p_cor[i] <- summary(M_cor)$coefficients[2, 4] #p-value из summary модели 
 }
```

]

Для простого "шума", когда нет автокорреляций и нет связи между `$y$` и `$x$` (справедлива `$H_0$`) частота ошибок составляет

``` r
mean(p_values$p_no_cor < 0.05)
```

```
[1] 0.048
```
]
--
.pull-right-40[
Для автокоррелированных данных, при отсутствии связи между  `$y$` и `$x$` (справедлива `$H_0$`) частота ошибок составляет

``` r
mean(p_values$p_cor < 0.05)
```

```
[1] 0.233
```
]

---

## Проверка на автокорреляцию

Проверка на автокорреляцию нужна, если данные --- это временной ряд, или если известны координаты или время сбора проб. Способы проверки временной автокорреляции (годятся, если наблюдения в ряду расположены через равные интервалы):

- График автокорреляционной функции остатков (ACF-plot) покажет корреляции с разными лагами.

![](07_model_description_and_validation_files/figure-html/unnamed-chunk-22-1.png)

- Критерий Дарбина-Уотсона (значимость автокорреляции 1-го порядка).

Для проверки пространственных автокорреляций: *вариограммы*

---

## Что делать, если у вас нарушено условие независимости значений?

Выбор зависит от обстоятельств. Вот несколько возможных вариантов.

+ псевдоповторности
    - избавляемся от псевдоповторностей, вычислив среднее
    - подбираем смешанную модель (модель со случайным фактором)
+ неучтенные переменные
    - включаем в модель (если возможно)
+ временные автокорреляции
    - моделируем автокорреляцию
    - подбираем модель со случайным фактором
+ пространственные автокорреляции
    - моделируем пространственную автокорреляцию
    - делим на пространственные блоки и подбираем модель со случайным фактором (= random effects model, mixed model)

---

## Проверка условия независимости

### Графики зависимости остатков от предикторов в модели

``` r
# Полный код
ggplot(data = brain_diag, aes(x = MRINACount, y = .stdresid)) + 
  geom_point() + 
  geom_hline(yintercept = 0)
```

![](07_model_description_and_validation_files/figure-html/resid-predict-1.png)

``` r
# То же самое с использованием ранее созданного gg_resid
gg_resid + aes(x =  MRINACount)
```

---

### Графики зависимости остатков от предикторов не в модели

В данном случае их нет

---

# 3. Нормальное распределение

---

## 3. Нормальное распределение `$y$` (для каждого уровня значений `$x$`)

![](07_model_description_and_validation_files/figure-html/gg-norm-tunnel-1.png)

]

Это условие невозможно проверить "в лоб", т.к. обычно каждому `$x$` соответствует лишь небольшое число `$y$`

]

---

## Проверка нормальности распределения остатков

Если `$y$` это нормально распределенная случайная величина

`$$y_i \sim N(\mu_{y_i}, \sigma)$$`

и мы моделируем ее как

`$$y_i = b_0 + b_1x_{1i} + \cdots + e_i$$`

то остатки от этой модели — тоже нормально распределенная случайная величина

`$$e_i \sim N(0, \sigma)$$`

Т.е. выполнение этого условия можно оценить по поведению случайной части модели.

---

## Проверка нормальности распределения остатков

Есть формальные тесты, но:

- у формальных тестов тоже есть свои условия применимости
- при больших выборках формальные тесты покажут, что значимы даже небольшие отклонения от нормального распределения
- тесты, которые используются в линейной регрессии, устойчивы к небольшим отклонениям от нормального распределения

Лучший способ проверки — квантильный график остатков.

---

## Квантильный график остатков

По оси Х — квантили теоретического распределения, по оси Y — квантили остатков модели. Если наблюдаемое распределение соответствует теоретическому, то точки должны лечь вдоль прямой по диагонали графика.

Обычные остатки должны подчиняться нормальному распределению `$e \sim N(0, \sigma)$`

Cтьюдентизированные остатки — t-распределению

``` r
# library(car)
qqPlot(brain_model, id = FALSE) # из пакета car
```

![](07_model_description_and_validation_files/figure-html/qqplot-1.png)

---

## Что делать, если остатки распределены не нормально?

Зависит от причины

- Нелинейная связь?
    - Построить аддитивную модель (если достаточно наблюдений по `$x$`)
    - Построить нелинейную модель (если известна форма зависимости)
- Неучтенные переменные?
    - добавляем в модель
- Зависимая переменная распределена по-другому?
    - трансформируем данные (неудобно)
    - подбираем модель с другим распределением остатков (обобщенную линейную модель)

---

# 4. Постоянство дисперсии

---

## 4. Постоянство дисперсии (= гомогенность дисперсии, гомоскедастичность)

![](07_model_description_and_validation_files/figure-html/gg-norm-tunnel-1.png)

]
.pull-right-40[

Это самое важное условие, поскольку многие тесты чувствительны к гетероскедастичности.

]

---

## Проверка гомогенности дисперсий

Есть формальные тесты (тест Бройша-Пагана, тест Кокрана), но:

- у формальных тестов тоже есть свои условия применимости, и многие сами неустойчивы к гетероскедастичности
- при больших выборках формальные тесты покажут, что значима даже небольшая гетероскедастичность

Лучший способ проверки на гомогенность дисперсий — график остатков от предсказанных значений.

---

## Проверка гомогенности дисперсий

![](07_model_description_and_validation_files/figure-html/homo-hetero-1.png)

---

## Чем опасна гетероскедастичность

Создадим две генеральные совокупности, в которых нет связи между `$y$` и `$x$`
![](07_model_description_and_validation_files/figure-html/unnamed-chunk-24-1.png)

---

## Чем опасна гетероскедастичность

.pull-left-60[
Возьмем 1000 выборок из этих совокупностей по 10 наблюдений и построим много линейных моделей

``` r
p_values <- data.frame(p_no_heter = rep(NA, 1000), p_heter = NA)

for(i in 1:1000){
 df <- dat2[sample(1:1000, 10), ]
 M_no_heter <- lm(y_1 ~ x, data = df)
 M_heter <- lm(y_2 ~ x, data = df)
 p_values$p_no_heter[i] <- summary(M_no_heter)$coefficients[2, 4] #p-value из summary модели 
 p_values$p_heter[i] <- summary(M_heter)$coefficients[2, 4] #p-value из summary модели 
 }
```
]

- Нет гетероскедастичности и нет связи между `$y$` и `$x$` (справедлива `$H_0$`) частота ошибок составляет

``` r
mean(p_values$p_no_heter < 0.05)
```

```
[1] 0.039
```
]
.pull-right-40[

- Для совокупности с гетероскедастичностью, при отсутствии связи между  `$y$` и `$x$` (справедлива `$H_0$`) частота ошибок составляет

``` r
mean(p_values$p_heter < 0.05)
```

```
[1] 0.073
```
]

---

## Проверка на гетероскедастичность

Этот график у нас уже есть

``` r
gg_resid
```

![](07_model_description_and_validation_files/figure-html/resid-plot-1.png)

- Гетерогенность дисперсий не выражена.

---

## Что делать, если найдена гетероскедастичность?

![](07_model_description_and_validation_files/figure-html/hetero-log-transform-1.png)

Трансформация может помочь, но лучше изменить модель.

---

## Возможные причины гетероскедастичности

Даже если трансформация может помочь, лучше поискать причину гетерогенности дисперсий

- Неучтенные переменные
    - добавляем в модель
- Зависимая переменная распределена по-другому
    - трансформируем данные (неудобно)
    - подбираем модель с другим распределением остатков (обобщенную линейную модель)
- Моделируем гетерогенность дисперсии.

---

# Тренинг по анализу остатков

---

## Некоторые частые паттерны на графиках остатков

![:scale 100%](images/Residuals.png)

]

- Рис. a — Условия применимости соблюдаются, модель хорошая

- Рис. b — Клиновидный паттерн. Есть гетероскедастичность. Модель плохая

- Рис. c — Остатки рассеяны равномерно, но нужны дополнительные предикторы

- Рис. d — Нелинейный паттерн. Линейная модель использована некорректно

]

---

## Задание 3

Выполните три блока кода

Какие нарушения условий применимости линейных моделей здесь наблюдаются?

Вам понадобятся

1. График расстояния Кука
2. График остатков от предсказанных значений
3. Графики остатков от предикторов в модели и не в модели
4. Квантильный график остатков

---

## Задание 3, блок 1

``` r
set.seed(90829)
x1 <- seq(1, 100, 1)
y1 <- diffinv(rnorm(99)) + rnorm(100, 0.2, 4)
dat1 = data.frame(x1, y1)
ggplot(dat1, aes(x = x1, y = y1)) + geom_point()+ 
 geom_smooth(method="lm", alpha = 0.7)
```

![](07_model_description_and_validation_files/figure-html/block-1-task-1.png)

---

## Решение, блок 1

### Графики

![](07_model_description_and_validation_files/figure-html/block-1-1.png)

- Выбросов нет, зависимость нелинейна
- Небольшие отклонения от нормального распределения

---

## Решение, блок 1

``` r
mod1 <- lm(y1 ~ x1, data = dat1)

# Данные для графиков остатков
mod1_diag <- fortify(mod1)

# 1) График расстояния Кука
ggplot(mod1_diag, aes(x = 1:nrow(mod1_diag), y = .cooksd)) + 
  geom_bar(stat = "identity")

# 2) График остатков от предсказанных значений
gg_resid <- ggplot(data = mod1_diag, aes(x = .fitted, y = .stdresid)) + 
 geom_point() + geom_hline(yintercept = 0)
gg_resid

# 3) Графики остатков от предикторов в модели и не в модели
gg_resid + aes(x = x1)

# 4) Квантильный график остатков
qqPlot(mod1, id = FALSE)       
```

---

## Задание 3, блок 2

``` r
 set.seed(7657674)
 x2 <- runif(1000, 1, 100)
 b_0 <- 100; b_1 <- -20
 h <- function(x) x^0.5
 eps <- rnorm(1000, 0, h(x2))
 y2 <- b_0 + b_1 * x2 + eps
 dat2 <- data.frame(x2, y2)
 ggplot(dat2, aes(x = x2, y = y2)) + 
 geom_point() + 
 geom_smooth(method = "lm")
```

![](07_model_description_and_validation_files/figure-html/block-2-task-1.png)

---

## Решение, блок 2

![](07_model_description_and_validation_files/figure-html/block-2-1.png)

- Выбросов нет
- Гетерогенность дисперсий, остатки не подчиняются нормальному распределению

---

## Решение, блок 2

``` r
mod2 <- lm(y2 ~ x2, data = dat2)

# Данные для графиков остатков
mod2_diag <- fortify(mod2)

# 1) График расстояния Кука
ggplot(mod2_diag, aes(x = 1:nrow(mod2_diag), y = .cooksd)) + 
  geom_bar(stat = "identity")

# 2) График остатков от предсказанных значений
gg_resid <- ggplot(data = mod2_diag, aes(x = .fitted, y = .stdresid)) + 
 geom_point() + geom_hline(yintercept = 0)
gg_resid

# 3) Графики остатков от предикторов в модели и не в модели
gg_resid + aes(x = x2)

# 4) Квантильный график остатков
qqPlot(mod2, id = FALSE)       
```

---

## Задание 3, блок 3

``` r
set.seed(9283)
x3 <- rnorm(25, 50, 10)
b_0 <- 20; b_1 <- 20; eps <- rnorm(50, 0, 100)
y3 <- b_0 + b_1*x3 + eps
y3[100] <- 1000; x3[100] <- 95; y3[99] <- 1300; x3[99] <- 90; y3[98] <- 1500; x3[98] <- 80
dat3 <- data.frame(x3, y3)
ggplot(dat3, aes(x=x3, y=y3)) + geom_point() + geom_smooth(method="lm")
```

![](07_model_description_and_validation_files/figure-html/block-3-task-1.png)

---

## Решение, блок 3

![](07_model_description_and_validation_files/figure-html/block-3-1.png)

- 100-е наблюдение сильно влияет на ход регрессии
- Зависимость может быть нелинейна

---

## Решение, блок 3

``` r
mod3 <- lm(y3 ~ x3, data = dat3)

# Данные для графиков остатков
mod3_diag <- fortify(mod3)

# 1) График расстояния Кука
ggplot(mod3_diag, aes(x = 1:nrow(mod3_diag), y = .cooksd)) + 
  geom_bar(stat = "identity")

# 2) График остатков от предсказанных значений
gg_resid <- ggplot(data = mod3_diag, aes(x = .fitted, y = .stdresid)) + 
 geom_point() + geom_hline(yintercept = 0)
gg_resid

# 3) Графики остатков от предикторов в модели и не в модели
gg_resid + aes(x = x3)

# 4) Квантильный график остатков
qqPlot(mod3, id = FALSE)       
```

---

## Задание 4

Выполните последнее задание в одном из этих файлов:
- 07_task_assumptions_catsM.R
- 07_task_assumptions_GAG.R

---

## Take-home messages

- Гипотезы о наличии зависимости можно тестировать при помощи t- или F-теста.
- Качество подгонки модели можно оценить при помощи коэффициента детерминации `$R^2$`.

- У линейных моделей есть условия применимости, поэтому не спешите описывать результаты — сначала проверьте.

- Если условия применимости нарушены, то результатам тестов для этой модели нельзя верить (получаются заниженные доверительные вероятности, возрастает вероятность ошибок I рода).
- Анализ остатков дает разностороннюю информацию о валидности моделей.

---

## Что почитать

+ Гланц, С., 1998. Медико-биологическая статистика. М., Практика
+ Кабаков Р.И. R в действии. Анализ и визуализация данных на языке R. М.: ДМК Пресс, 2014
+ Diez, D.M., Barr, C.D. and Çetinkaya-Rundel, M., 2015. OpenIntro Statistics. OpenIntro.
+ Zuur, A., Ieno, E.N. and Smith, G.M., 2007. Analyzing ecological data. Springer Science & Business Media.
+ Quinn G.P., Keough M.J. 2002. Experimental design and data analysis for biologists
+ Logan M. 2010. Biostatistical Design and Analysis Using R. A Practical Guide