class: middle, left, inverse, title-slide .title[ # Работа с распределениями ] .subtitle[ ## Линейные модели в R ] .author[ ### Марина Варфоломеева ] .author[ ### Вадим Хайтов ] .author[ ### Юта Тамберг ] .author[ ### Анастасия Лянгузова ] --- class: middle, center, inverse .right[Целью моделирования является получение] .right[простых суммарных (сводных, итоговых)] .right[характеристик набора данных.] .right[(Уикем, Гроулмунд, 2018)] # Модель нормального распределения --- ## Как передать информацию о большом наборе данных? ```r set.seed(12345) dat <- round(rnorm(100, 10, 2), 1) dat ``` ``` ## [1] 11.2 11.4 9.8 9.1 11.2 6.4 11.3 9.4 9.4 8.2 9.8 13.6 10.7 ## [14] 11.0 8.5 11.6 8.2 9.3 12.2 10.6 11.6 12.9 8.7 6.9 6.8 13.6 ## [27] 9.0 11.2 11.2 9.7 11.6 14.4 14.1 13.3 10.5 11.0 9.4 6.7 13.5 ## [40] 10.1 12.3 5.2 7.9 11.9 11.7 12.9 7.2 11.1 11.2 7.4 8.9 13.9 ## [53] 10.1 10.7 8.7 10.6 11.4 11.6 14.3 5.3 10.3 7.3 11.1 13.2 8.8 ## [66] 6.3 11.8 13.2 11.0 7.4 10.1 8.4 7.9 14.7 12.8 11.9 11.7 8.4 ## [79] 11.0 12.0 11.3 12.1 9.4 15.0 11.9 13.7 11.3 9.4 11.1 11.6 8.1 ## [92] 8.3 13.8 9.2 8.0 11.4 9.0 14.3 8.8 8.6 ``` --- ## Способ 1. Можно построить график. .pull-left-40[ ```r df <- data.frame(X = dat) Pl <- df %>% ggplot() Pl + geom_histogram(aes(x = X), bins = 10) ``` 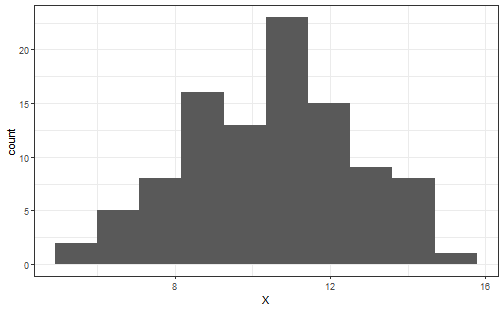<!-- --> ] .pull-right-40[ ```r Pl + geom_boxplot(aes(y = X)) ``` 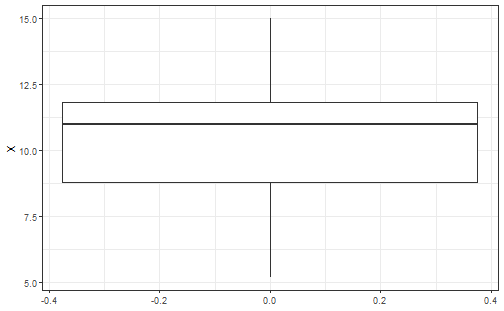<!-- --> ] --- ## Способ 2. Можно охарактеризовать медиану и квартили. ```r summary(dat) ``` ``` ## Min. 1st Qu. Median Mean 3rd Qu. Max. ## 5.2 8.8 11.0 10.5 11.8 15.0 ``` Можно ли по этим данным "воспроизвести" исходный ряд? --- ## Способ 3. Можно смоделировать данные .pull-left-40[ 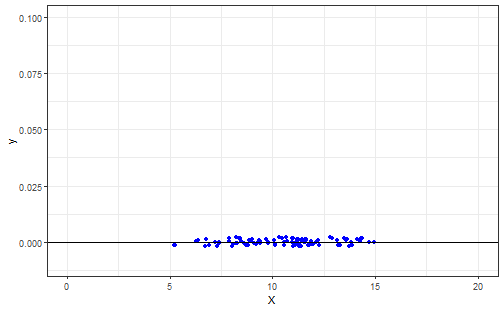<!-- --> ] .pull-right-40[ 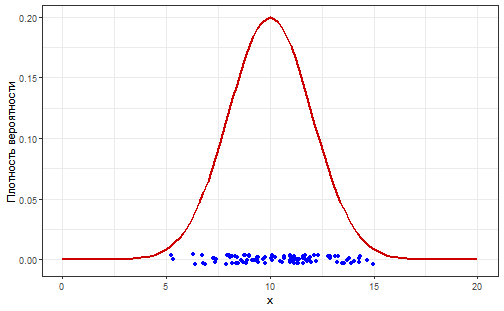<!-- --> ] Эта модель описывается всего двумя числами $$ \mu = 10 \\ \sigma = 2 $$ Можно ли по этим данным "воспроизвести" исходный ряд? --- ## "Реконструируем" ряд по данным из модели <img src="03.2_descriptive_statistics_normal_d_version_2023_files/figure-html/unnamed-chunk-7-1.png" style="display: block; margin: auto;" /> --- ## Нормальное, или Гауссово, распределение .center[] --- ## Нормальное распределение .pull-left-66[ <!-- --> ] .pull-right-33[ - симметричное - унимодальное - непрерывное ] .pull-left-66[ `$$f(x) = \cfrac {1}{\sigma \sqrt{2 \pi}} \; e^{- \: \cfrac{(x-\mu)^2}{2\sigma^2}}$$` - `\(\mu\)` --- среднее значение; - `\(\sigma\)` --- стандартное отклонение. Это кратко записывается как `\(x \sim N(\mu, \sigma)\)`. ] --- ## Смысл параметров нормального распределения <!-- --> .pull-left[ $$ \mu_A = \mu_C ; \sigma_A > \sigma_C $$ ] .pull-right[ $$ \mu_B < \mu_D ; \sigma_B = \sigma_D $$ ] --- ## Стандартное нормальное распределение <!-- --> `$$N(0, 1)$$` Зачем нужно стандартизованное распределение? -- Квантили в нормальном распределении зависят от `\(\mu\)` и `\(\sigma\)` и могут быть любыми. В **стандартизованном распределении** квантили строго определены! Это свойство используется для построения *статистических тестов*. --- ## Квантили стандартизованного нормального распределения ```r round(qnorm(p = c(0.025, 0.975), mean = 0, sd = 1), 2) ``` ``` ## [1] -1.96 1.96 ``` ```r round(qnorm(p = c(0.95), mean = 0, sd = 1), 2) ``` ``` ## [1] 1.64 ``` Запомните эти числа на будущее! --- ## Стандартизация рспределения (Z-преобразование) .pull-left[ <!-- --> ] .pull-right[ `$$z = \frac{x - \mu}{\sigma}$$` После стандартизации любое нормальное распределение превращается в стандартное нормальное: `$$Z \sim N(0, 1)$$` ] --- ## Стандартизация векторов .pull-left[ <!-- --> ] .pull-right[ `$$z_i=\frac{x_i - \bar{x}}{sd}$$` Стандартизованная величина (Z-оценка) показывает, на сколько стандартных отклонений значение отличается от среднего **После стандартизации всегда**: - среднее `\(\bar{z} = 0\)` - стандартное отклонение `\(sd_{z} = 1\)` ] Зачем это нужно? -- Стандартизация векторов применяется для их сравнения с предсказаниями модели стандартизованного нормального распределения. --- ## Задание 1 - Стандартизуйте вектор `1:5` - Вычислите среднее значение стандартизованного вектора? - Вычислите стандартное отклонение стандартизованного вектора? --- class: middle, center, inverse # Проверка на нормальность --- ## Квантильный график По оси `\(X\)` отложены квантили стандартного нормального распределения, по оси `\(Y\)` --- квантили данных. Если `\(x \sim N(\mu,\sigma)\)`, то точки лягут на прямую линию. <!-- --> --- ## Квантильный график вручную .pull-left[ ```r norm_q <- qnorm(p = seq(0.01, 0.99, 0.01), mean = 0, sd = 1) observ_q <- quantile(x, probs = seq(0.01, 0.99, 0.01)) ``` ] .pull-right[ <!-- --> ] --- ## Квантильный график в `R` ```r set.seed(9128) my_vector <- rnorm(n = 150, mean = 10, sd = 3) library(car) qqPlot(my_vector, id = FALSE) # квантильный график ``` <!-- --> --- ## Задание 2 Выполните по одному блоки кода (см. код к этой презентации). Что вы можете сказать о свойствах распределений, изображенных на квантильных графиках? --- ## Бимодальное (двувершинное) распределение <!-- --> --- ## Дискретное распределение с длинным правым хвостом <!-- --> --- ## Непрерывное распределение с толстыми хвостами <!-- --> --- ## Непрерывное распределение с длинным правым хвостом <!-- --> <!-- Если интересны подробности, можно посмотреть симуляции, например, здесь https://stats.stackexchange.com/questions/101274/how-to-interpret-a-qq-plot --> --- ## Задание 3 Проверьте при помощи квантильного графика, подчиняются ли эти переменные нормальному распределению: - Рост американских женщин (датасет `women`) - Длина чашелистиков у ирисов (датасет `iris`) - Число пойманных рысей в Канаде с 1821 по 1934г. (датасет `lynx`) --- ## Решение (3.1) ```r data("women") str(women) ``` ``` ## 'data.frame': 15 obs. of 2 variables: ## $ height: num 58 59 60 61 62 63 64 65 66 67 ... ## $ weight: num 115 117 120 123 126 129 132 135 139 142 ... ``` ```r qqPlot(women$height, id = FALSE) ``` <!-- --> --- ## Решение (3.2) ```r data("iris") str(iris) ``` ``` ## 'data.frame': 150 obs. of 5 variables: ## $ Sepal.Length: num 5.1 4.9 4.7 4.6 5 5.4 4.6 5 4.4 4.9 ... ## $ Sepal.Width : num 3.5 3 3.2 3.1 3.6 3.9 3.4 3.4 2.9 3.1 ... ## $ Petal.Length: num 1.4 1.4 1.3 1.5 1.4 1.7 1.4 1.5 1.4 1.5 ... ## $ Petal.Width : num 0.2 0.2 0.2 0.2 0.2 0.4 0.3 0.2 0.2 0.1 ... ## $ Species : Factor w/ 3 levels "setosa","versicolor",..: 1 1 1 1 1 1 1 1 1 1 ... ``` ```r op <- par(mfrow = c(1, 2)) qqPlot(iris$Sepal.Length, id = FALSE) hist(iris$Sepal.Length) ``` <!-- --> ```r par(op) ``` --- ## Решение (3.3) ```r data("lynx") str(lynx) ``` ``` ## Time-Series [1:114] from 1821 to 1934: 269 321 585 871 1475 ... ``` ```r op <- par(mfrow = c(1, 2)) qqPlot(lynx, id = FALSE) hist(lynx) ``` <!-- --> ```r par(op) ``` --- class: middle, center, inverse # Оценка вероятностей при помощи распределений --- ## Эмпирическое правило нормального распределения .center[  ] - 68% значений находятся в пределах 1 стандартного отклонения `\(\sigma\)` - 95% значений --- в пределах 2 `\(\sigma\)` - 99.7% значений --- в пределах 3 `\(\sigma\)` --- ## Модель нормального распределения позволяет оценивать вероятности событий ### Вероятности --- это площади под кривой распределения <!-- --> `\(-\infty < x < +\infty\)`. Площадь под всей кривой `\(= 1\)`. Вероятность встречи значений из определенного промежутка можно узнать, проинтегрировав функцию распределения. --- ## Кривые распределений можно использовать для оценки вероятностей <!-- --> --- ## Площадь под всей кривой распределения равна 1 <!-- --> --- ## Вероятность конкретного значения нельзя определить <!-- --> --- ## Можно определить вероятность того, что значение будет меньше заданного <!-- --> --- ## Остальные площади легко найти при помощи простых арифметических действий с площадями <!-- --> --- ## Пример: Размеры улиток Cредний диаметр раковины улиток в популяции 5 см, стандартное отклонение 1.5 см. - Какова вероятность того, что случайно выбранная улитка окажется __меньше 3 см__? - Какова вероятность того, что случайно выбранная улитка окажется __больше 6 см__? - Какова доля улиток с размером раковины __в пределах 3--6 см__? .center['] .right[<small>tres caracoles by Alberto Villen on Freeimages.com</small>] --- ## Вероятность встретить значение меньше заданного В выборке улиток средний диаметр раковины 5 см со стандартным отклонением 1.5 см. **Какова вероятность того, что случайно выбранная улитка окажется __меньше 3 см__?** ```r Z_1 <- (3 - 5) / 1.5 pnorm(q = Z_1) ``` ``` ## [1] 0.0912 ``` ```r # или то же самое pnorm(q = 3, mean = 5, sd = 1.5) ``` ``` ## [1] 0.0912 ``` <!-- --> --- ## Вероятность встретить значение больше заданного В выборке улиток средний диаметр раковины 5 см со стандартным отклонением 1.5 см. **Какова вероятность того, что случайно выбранная улитка окажется __больше 6 см__?** .pull-left-33[Мы умеем интегрировать только влево от выбранного значения, поэтому - выясняем вероятность встретить значение меньше заданного `\(p\)` - находим комплементарную вероятность `\(1 - p\)`] .pull-right-66[ ```r 1 - pnorm(q = 6, mean = 5, sd = 1.5) ``` ``` ## [1] 0.252 ``` <!-- --> ] --- ## Вероятность встретить значение в заданных пределах В выборке улиток средний диаметр раковины 5 см со стандартным отклонением 1.5 см. **Какова доля улиток с размером раковины __в пределах 3--6 см__?** ```r pnorm(q = 6, mean = 5, sd = 1.5) - pnorm(q = 3, mean = 5, sd = 1.5) ``` ``` ## [1] 0.656 ``` <!-- --> --- ## Задание 4 Средний рост 18-летних мужчин в России 174.7 см со стандартным отклонением 6.65 см. В пилоты берут только людей с ростом от 160 до 190 см (по приказу Минтранса). - Какова вероятность того, что случайно выбранный мужчина окажется __ниже 160 см__? - Какова вероятность того, что случайно выбранный мужчина окажется __больше 190 см__? - Какова доля мужчин, не подходящих по росту в пилоты, т.е. __меньше 160 и больше 190 см__? --- ## Решение (4.1) Средний рост 18-летних мужчин в России 174.7 см со стандартным отклонением 6.65 см. В пилоты берут только с ростом от 160 до 190 см (по приказу Минтранса). **Какова вероятность того, что случайно выбранный мужчина окажется __ниже 160 см__?** ```r Z_short <- (160 - 174.7) / 6.65 pnorm(q = Z_short) ``` ``` ## [1] 0.0135 ``` ```r # или то же самое pnorm(q = 160, mean = 174.7, sd = 6.65) ``` ``` ## [1] 0.0135 ``` <!-- --> --- ## Решение (4.2) Средний рост 18-летних мужчин в России 174.7 см со стандартным отклонением 6.65 см. В пилоты берут только с ростом от 160 до 190 см (по приказу Минтранса). **Какова вероятность того, что случайно выбранный мужчина окажется __больше 190 см__?** ```r 1 - pnorm(q = 190, mean = 174.7, sd = 6.65) ``` ``` ## [1] 0.0107 ``` <!-- --> --- ## Решение (4.3) Средний рост 18-летних мужчин в России 174.7 см со стандартным отклонением 6.65 см. В пилоты берут только с ростом от 160 до 190 см (по приказу Минтранса). **Какова доля мужчин, не подходящих по росту в пилоты, т.е. __меньше 160 и больше 190 см__?** ```r (1 - pnorm(q = 190, mean = 174.7, sd = 6.65)) + pnorm(q = 160, mean = 174.7, sd = 6.65) ``` ``` ## [1] 0.0242 ``` <!-- --> --- ## Задание 5 Средний рост девушек в популяции в 16 лет --- 162.2 см со стандартным отклонением 6.0 см. В пилоты берут только людей с ростом от 160 до 190 см (по приказу Минтранса). **Какой процент девушек подходит по росту в пилоты?** --- ## Решение Средний рост девушек в 16 лет --- 162.2 см со стандартным отклонением 6.0 см. В пилоты берут только людей с ростом от 160 до 190 см (по приказу Минтранса). **Какой процент девушек подходит по росту в пилоты?** ```r pnorm(q = 190, mean = 162.2, sd = 6.0) - pnorm(q = 160, mean = 162.2, sd = 6.0) ``` ``` ## [1] 0.643 ``` Только 64.3 % девушек пройдут в пилоты по росту. <!-- --> --- ## Задание 6 Предположим, что вес новорожденных нормально распределен со средним значением 3500 г и стандартным отклонением 600 г. - Какой процент детей рождается с весом больше 3200г.? - Какой процент детей рождается с весом в пределах 2500-4500г.? --- ## Решение (1) Предположим, что вес новорожденных нормально распределен со средним значением 3500 г и стандартным отклонением 600 г. **Какой процент детей рождается с весом больше 3200г.?** ```r 1 - pnorm(q = 3200, mean = 3500, sd = 600) ``` ``` ## [1] 0.691 ``` 69.1 % детей рождается с весом больше 3200г. <!-- --> --- ## Решение (2) Предположим, что вес новорожденных нормально распределен со средним значением 3500 г и стандартным отклонением 600 г. **Какой процент детей рождается с весом в пределах 2500-4500г.?** ```r pnorm(q = 4500, mean = 3500, sd = 600) - pnorm(q = 2500, mean = 3500, sd = 600) ``` ``` ## [1] 0.904 ``` 90.4 % детей рождается с весом в пределах 2500-4500г. <!-- --> --- ## Take-home messages - Нормальное распределение `\(N(\mu,\sigma)\)` - Стандартное нормальное распределение --- `\(N(0, 1)\)` - Стандартизация --- `\(z = \frac{x - \mu} {\sigma}\)` - Квантильный график --- графический метод проверки формы распределения - Вероятность попадания величины в любой интервал можно найти при помощи интегрирования - Выборочные оценки